14.4.2024 - Ing. Aleš Smeták
V tomto článku se podíváme na zoubek elektrickému výkonu v třífázové soustavě, také si něco řekneme o rozdílech výkonu v případě zapojení do hvězdy nebo do trojúhelníku a nakonec si ukážeme pár příkladů.
Zde si dovolím problematiku pro lepší pochopení velmi zjednodušit. Nejprve je nutné si uvědomit, že v síti máme vlastně tři proudy, které jsou proti sobě posunuté. Přesněji jsou posunuté o jednu třetinu periody respektive o 120°. Proud se vyrábí v generátorech, které mají tři cívky a každá cívka vyrábí jednu fázi. Toho lze třeba využít při vytváření točivého magnetického pole, které je základem všech elektromotorů (článek zde).
Některým spotřebičům pro jejich provoz bohatě postačuje kterákoliv zmíněná jedna "třetina" ze zmíněného generátoru. Tyto spotřebiče jsou pak určeny pro jednofázové rozvody (článek zde), ve kterých se proud vrací zpátky do zdroje nulovým vodičem. Jedná se zpravidla o spotřebiče s malým výkonem
Na rozdíl od jednofázové soustavy, v třífázové soustavě vstupují do hry všechny tři proudy ze všech tří cívek generátoru. Z tohoto důvodu jsou třífázové spotřebiče mnohem výkonější než spotřebiče jednofázové.
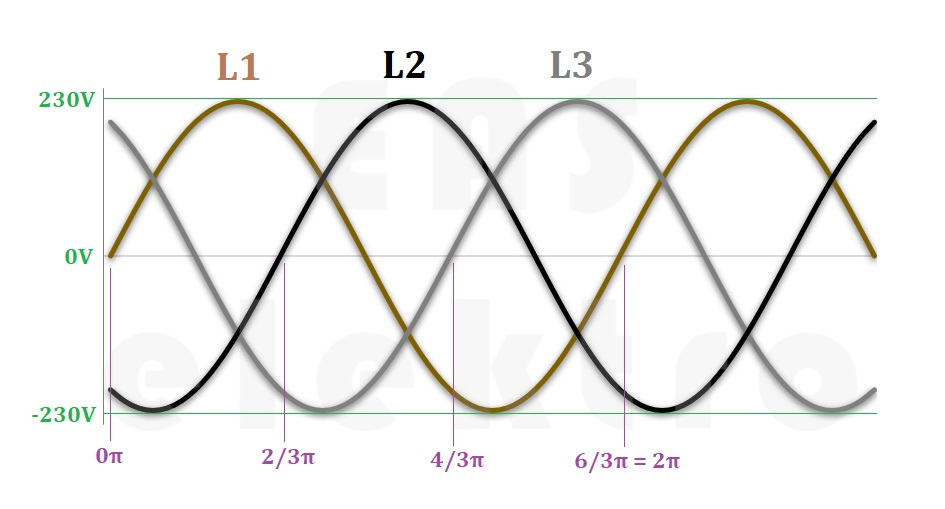
Na první pohled bychom mohli říct, že třífázový spotřebič bude třikrát silnější než spotřebič jednofázový... ano, ale může to být i víc.
Podívejme se pečlivě na obrázek niže s průběhem všech tří fází. Bavit se však budeme jen rozdílu napětí mezi fázemi L1 a L2. Z obrázku je patrné, že fáze L2 je o jednu třetinu posunutá oproti fázi L1 a nabývá proto v každém bodě jiné napětí než fáze L2. Zkusme blíže podívat na výše napětí v bodě označeném fialovou čárou, konkrétně v bodě 4π/3, a zde napětí fáze L1 = -200V a napětí fáze L2 = +200V. Rozdíl těchto napětí nazýváme jako sdružené napětí a v tomto bodě je rovno 400V. Naopak ve žlutě označeném bodě X bude sdružené napětí 0V, protože napětí L1 a L2 je stejné.
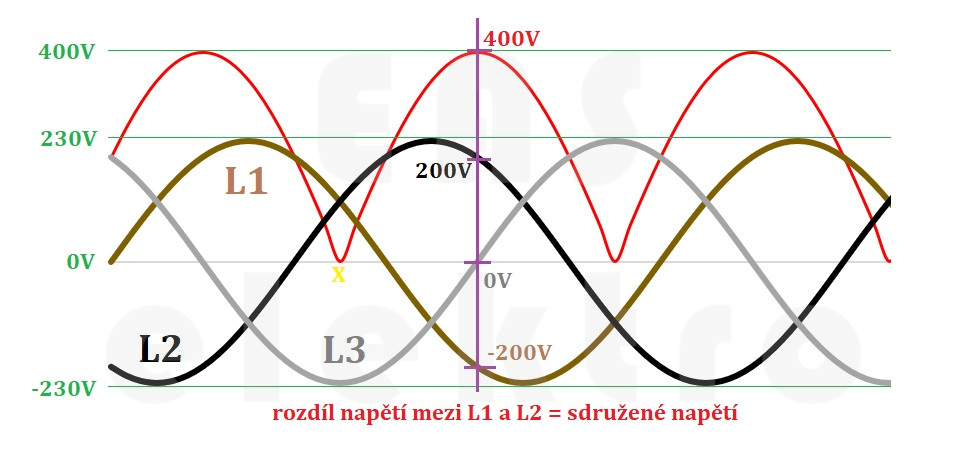
Úplně stejně bychom mohli řešit rozdíly mezi fázemi L1 a L3 a také mezi L2 a L3. I v těchto případech bychom zjistili, že rozdíl mezi jednotlivými fázovými napětími bude od 0V až po 400V.
Přesně s těmito sdruženými napětími mezi fázemi budeme pracovat v dalších částech kapitoly.
Z výše uvedeného výkladu si pozorný čtenář jistě uvědomil absurditu hospodské diskuze na téma, kdo kdy dostal větší ránu. Vždy se tam najde nějaký chytrolín, který chce ohromit osazenstvo tvrzením, že dostal od třífázové 3x230V/400V míchačky zásah neuvěřitelných 400V! Spíše tedy říkají jen 380V. Neumím si představit situaci, kdyby by průměrně inteligentní člověk nechtěně dostal "zásah" sdruženým napětím. Musel by totiž současně chytnout dva fázové vodiče a to může udělat s prominutím jen úplný blbec.
Pro zjednodušení budeme uvažovat se symetrickým (souměrným) zatížením jednotlivých fází, čili s tím, že všemi fázemi prochází stejný proud, protože všechny zátěže na nich mají stejnou impedanci*.
*) Impedance u střídavého napětí/proudu je to samé jako odpor u napětí/proudu stejnosměrného s tím rozdílem, že u stejnosměrného proudu je pouze činný odpor, kdežto impedance je vektorový součet činného a jalového odporu.
Zapojení do hvězdy (Y) je zapojení, při kterém využíváme sdružených a fázových napětí a jednoho proudu. Zapojení do hvězdy je vlastně to samé, jako kdybychom místo jednoho třífázového spotřebiče zapojili tři jednofázové.
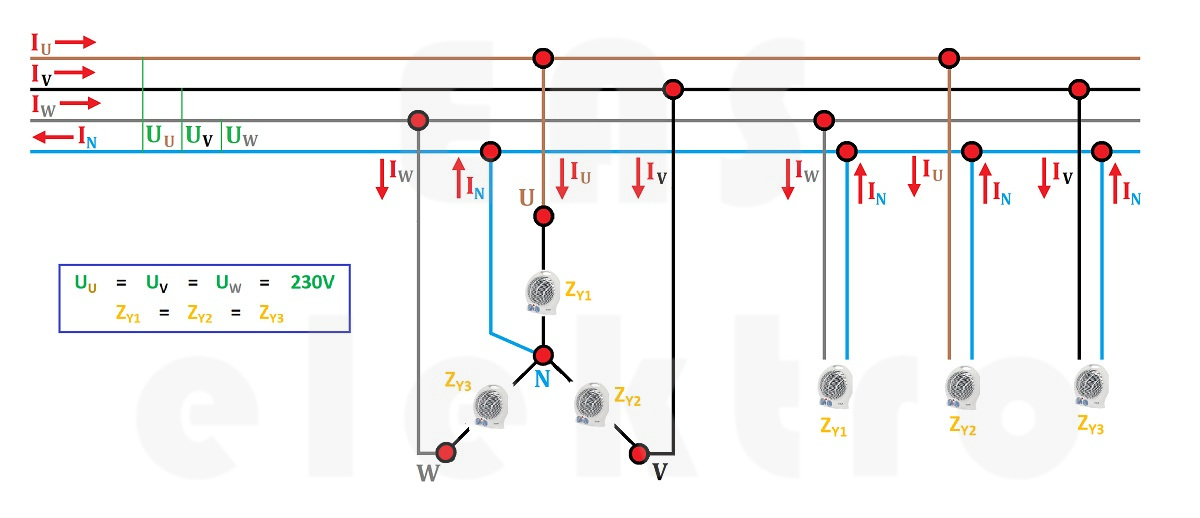
Při zapojení do hvězdy využíváme pouze fázových proudů Iu, Iv, Iw, které jsou stejné jako proud síťový. Pamatujme si, že při zapojení do hvězdy máme pouze jeden proud (Is) a dvě napětí - fázové (Uf) a sdružené (Us).
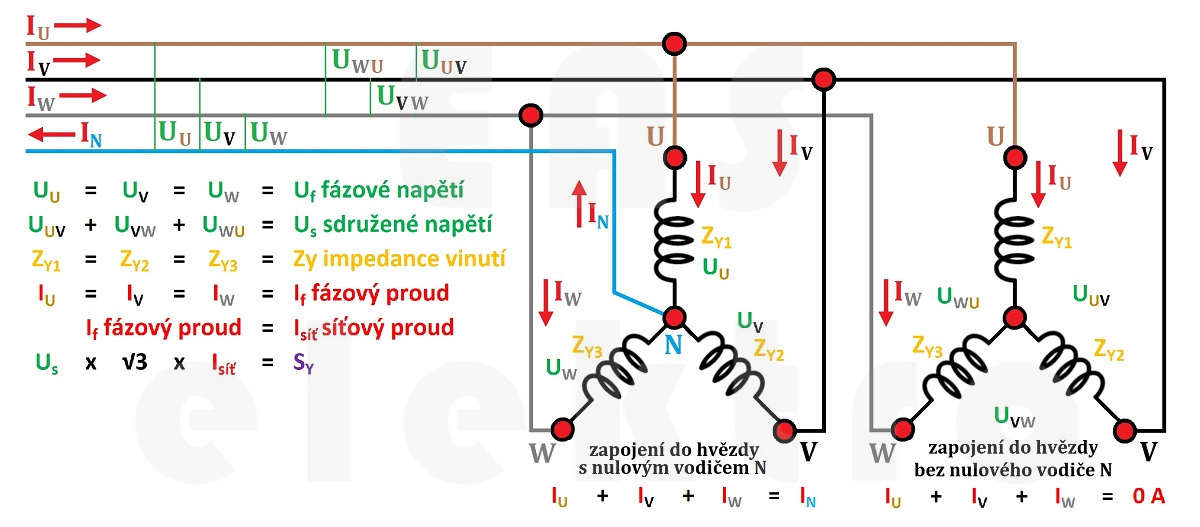
Zapojení do hvězdy může být provedeno s nulovým vodičem, ale i bez něj. Na funkci spotřebiče a další výpočty to nemá při správné funkci vliv. Případný rozdíl v zapojení se projeví při přerušení jedné fáze, viz příklad 8.

Výkon zátěže na jedné fázi pak spočítáme jako součin napětí a procházejícího proudu. Výkon celého spotřebiče pak bude trojnásobek výkonu jedné zátěže. O tom si řekneme více až dále...
Zapojení do trojúhelníku (
Δ
) je zapojení, při kterém naopak využíváme sdružených i fázových proudů a pouze jedno sdružené napětí. Pamatujme si, že při zapojení do trojúhleníku máme pouze jedno napětí a dva proudy - fázový (If) a sdružený (Is). Také si pamatujme, že proud fázový (If), který prochází vinutími, je menší než proud síťový (Is), který přichází do spotřebiče vodiči. V zapojení do trojúhelníku nenajdeme ani nulový vodič.
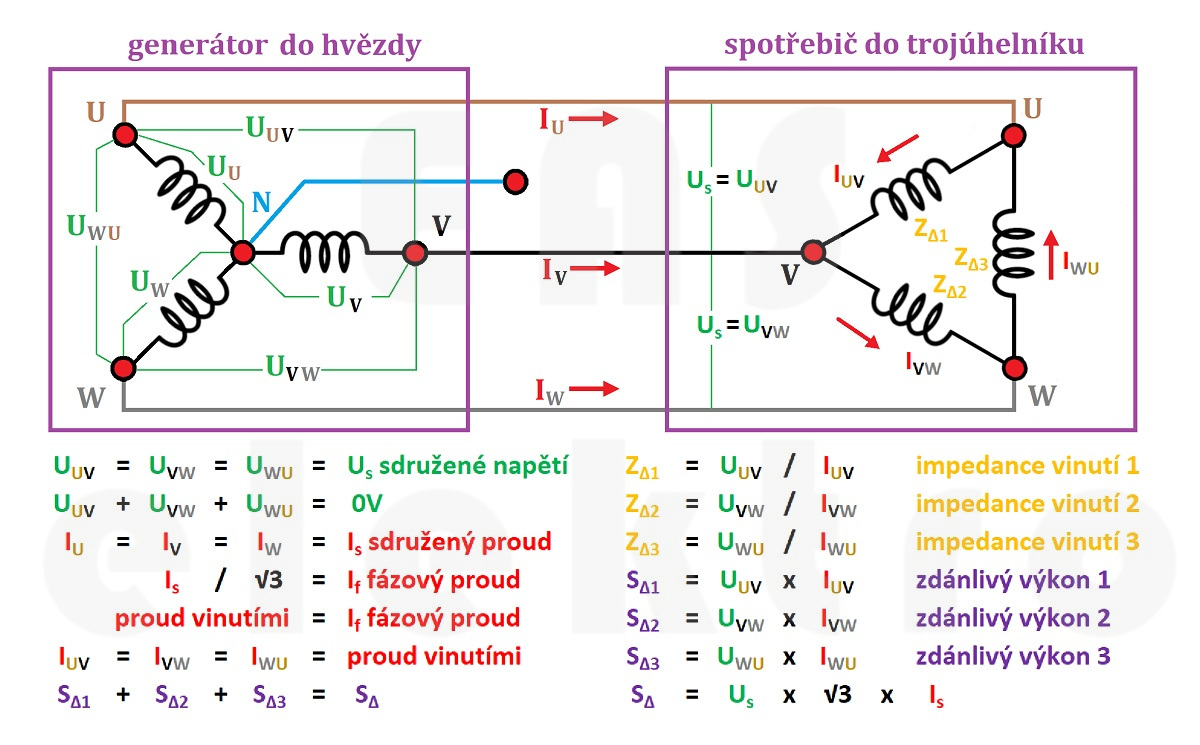
Výkon zátěže na jedné fázi pak spočítáme jako součin sdruženého napětí a procházejícího proudu. Výkon celého spotřebiče pak bude trojnásobek výkonu jedné zátěže. Ale i tom si řekneme více až dále...
Výpočet výkonu v třífázové soustavě pro zapojení ve hvězdě (Y) nebo v trojúhelníku (Δ) není nijak složitá záležitost, ale pro jeho správné pochopení je potřeba rozlišovat, jestli výpočet výkonu provádíme na základě napětí a proudů nebo na základě napětí a impedance zátěží.
Nejprve se podíváme na situaci, kdy výkon stanovujeme na základě měření procházejícího proudu spotřebičem a napětí na jeho svorkách.
V následujícím výkladu budeme uvažovat s naměřeným napětím 230V a protekájícím proudem 10A. Naším úkolem pak bude zjistit jaký výkon spotřebiče mají a jaký je odpor jednotlivých vinutí.
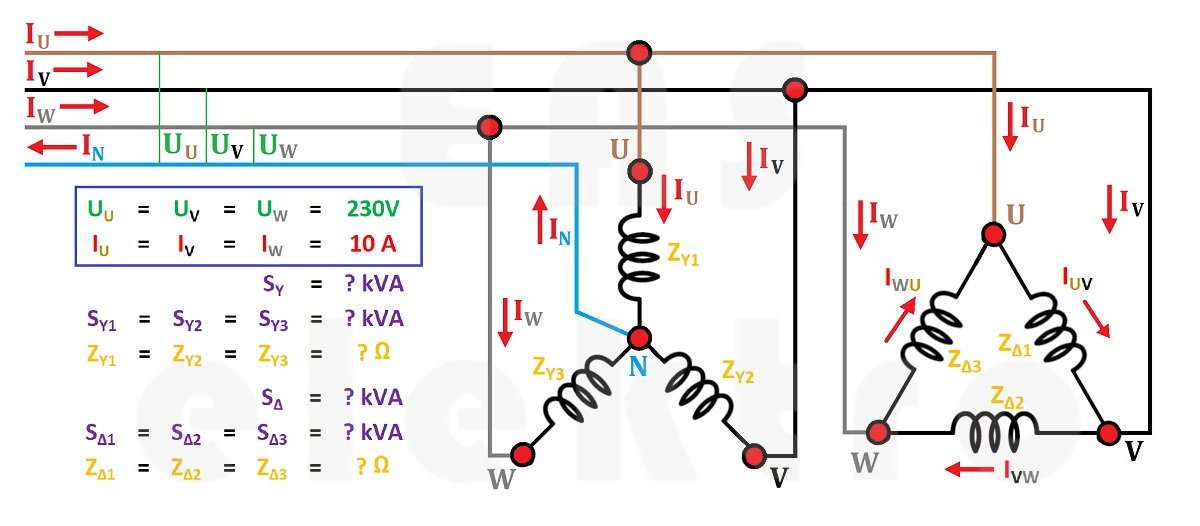
Začneme jednoduším zapojením do hvězdy Y (viz obrázek níže). Proud, který protéká vodiči na jednotlivé svorky spotřebiče (U,V,W) označujeme jako fázový/síťový (If/Isíť) a jeho výše je v našem případě 10A. Napětí, které můžeme naměřit mezi jednotlivými fázovými vodiči a nulovým vodičem označujeme jako fázové napětí (Uf) a jeho výše je v našem případě 230V.
Při znalosti fázového napětí už můžeme snadno zjistit i napětí sdružené (Us), které je součinem √3 a fázového napětím (Uf). V našem případě tedy okolo 400V.
Z výše uvedeného fázového napětí a proudu můžeme pomocí Ohmova zákona (článek zde) dopočítat impedanci jednotlivých vinutí (Zy). To bude tedy 230V / 10A = 23Ω.
Nebudeme si zatím komplikovat situaci účiníkem a zaměříme se jen zdánlivý výkon (S). Ten spočítáme jako součin fázového napětí (Uf) a procházejícího proudu vinutím (Isíť). To bude tedy 230V x 10A = 2,3 kVA. Ano, "kVA", protože zdánlivý výkon uvádíme ve voltampérech a nikoliv ve wattech.
No a protože máme vinutí tři, vynásobíme zdánlivý výkon jednoho vinutí třemi. To bude 3 x 2,3 kVA = 6,9 kVA.

Nyní se podíváme na zapojení do trojúhelníku Δ (viz obrázek níže). Proud, který protéká vodiči na jednotlivé svorky spotřebiče (U,V,W) označujeme jako sdružený (Is) a jeho výše je opět 10A. Napětí, které můžeme naměřit mezi jednotlivými fázovými vodiči označujeme jako sdružené napětí (Us) a jeho výše je v našem případě 400V. Nulový vodič v tomto zapojení nenajdeme a proto nemůže existovat ani fázové napětí (Uf).
Při znalosti sdruženého proudu (Is) můžeme snadno zjistit i výši fázového proudu (If) procházejícího vinutími, který je, podílem sdruženého proudu (Is) a √3. V našem případě tedy okolo 5,8A.
Z výše uvedeného fázového napětí a fázového proudu můžeme opět pomocí Ohmova zákona (článek zde) dopočítat impedanci jednotlivých vinutí (ZΔ). To bude tedy 400V / 5,8A = 69Ω.
Opět se nebudeme zabývat účiníkem a zaměříme se jen zdánlivý výkon (S). Ten spočítáme jako součin napětí (Us) a procházejícího proudu vinutím (If). To bude tedy 400V x 5,8A = 2,3 kVA.
No a protože zase máme tři vinutí, vynásobíme zdánlivý výkon jednoho vinutí třemi. To bude 3 x 2,3 kVA = 6,9 kVA.

Co si z této kapitoly můžeme odnést?
Pozorný čtenář si jistě všiml, že pro výpočet výkonu v třífázové síti je na obrázcích uveden ještě jeden vzorec, který využívá sdružených hodnot napětí i proudů a také si všiml, že tento vzorec je identický pro zapojení do hvězdy i do trojúhelníku.
To pochopitelně není náhoda... V této kapitole jsme se řešili výkon třífázového spotřebiče, do kterého tekl pořád stejný proud 10A při stejném napětí 230V a Jediné, co se měnilo, byl způsob zapojení. Zdánlivý výkon byl v obou případech zapojení stejný.
Je tomu skutečně tak. Vždyť by to popíralo fyzikální zákony, aby se výkon spotřebiče měnil je na základě způsobu jeho zapojení, pokud do něj teče pořád ten samý proud při stejném napětí. Energii si prostě z prstu nevycucáte...
Co tedy nebylo stejné? Byly to přece impedance jednotlivých zátěží/vinutí, které při zapojení do hvězdy měly jen 23Ω a při zapojení do trojúhelníku 69Ω, tedy 3x tolik.
Možná vám to přijde celé divné a říkáte si, k čemu je tedy dobré přepínaní motoru z hvězdy na trojúhelník. Máte samozřejmě pravdu, protože motor při zapojení do trojúhelníku má lidově řečeno větší záběr než při zapojení do hvězdy, ale taky častěji shazuje jističe. Přesně tomu se budeme věnovat v následující kapitole.
Tady už to bude zajímavější a malinko složitější. Zkusíme si vysvětlit, proč motor zapojený do hvězdy má menší výkon než motor zapojený do trojúhelníku. Abychom si však stále nemotali hlavu, nebudeme se účiníkem zatím ještě zabývat.
V následujícím výkladu budeme uvažovat s naměřeným napětím 230V, ale protože se jedná o motor, který nemůže měnit impedanci svých vinutí, budeme uvažovat jejich pevnou výši 23Ω. Tato impedance pak logicky musí být stejná při zapojení do hvězdy (Y) i při zapojení do trojúhelníku (Δ). Naším úkolem pak bude zjistit protékající proud (If nebo Is) a zdánlivý výkon (S) motoru.
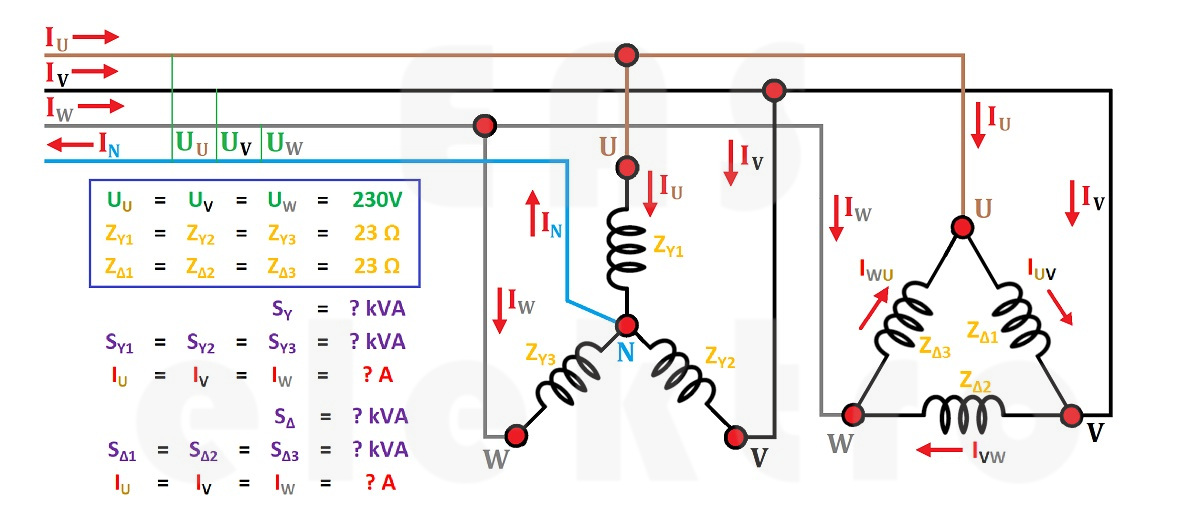
Začněme opět jednoduším zapojením do hvězdy Y (viz obrázek níže). Napětí, které můžeme naměřit mezi jednotlivými fázovými vodiči a nulovým vodičem označujeme jako fázové napětí (Uf) a jeho výše je zase 230V. Impedanci vinutí (Zy) známe ze zadání a je 23Ω.
Proud, který protéká vodiči na jednotlivé svorky spotřebiče (U,V,W) označujeme jako fázový/síťový (If/Isíť) a jeho výši dopočítáme pomocí Ohmova zákona (článek zde). To bude tedy 230V / 23Ω = 10A.
Z výše uvedeného fázového napětí a proudu můžeme již dopočítat zdánlivý výkon (S). Ten spočítáme jako součin fázového napětí (Uf) a procházejícího proudu vinutím (Isíť). To bude tedy 230V x 10A = 2,3 kVA. Opět vynásobíme zdánlivý výkon jednoho vinutí třemi a to bude 3 x 2,3 kVA = 6,9 kVA.
Nikoho asi nepřekvapí, že jsme se dopočítali ke stejnému výkonu jako v předchozí kapitole. No ještě aby ne, když se nic nezměnilo. Napětí zůstalo 230V a proud jsme dopočítali na původních 10A. Teď už to ovšem začne být zajímavější...

Pokračujme zapojením do trojúhelníku Δ (viz obrázek níže). Napětí, které můžeme naměřit mezi jednotlivými fázovými vodiči označujeme jako sdružené napětí (Us) a jeho výše je zase 400V. Impedanci vinutí (ZΔ) známe ze zadání a je stále 23Ω. Nulový vodič se v tomto zapojení nevyskytuje a proto ani nemůže existovat fázové napětí (Uf).
Proud, který protéká vodiči na jednotlivé svorky spotřebiče (U,V,W) označujeme jako sdružený a proud, který protéká jednotlivými vinutími označujeme jako proud fázový (If). Výši fázového proudu zjistíme opět pomocí Ohmova zákona (článek zde) a bude to 400V / 23Ω = 17,4A. A ejhle... první zásadní změna. Poměrně zásadní nárůst proudu. Zkusíme si ještě dopočítat sdružený proud (Is), který poteče vodiči na svorky motoru (U,V,W). Ten bude ve výši součinu √3 x If = 30,1A.
Z výše uvedeného napětí a proudu můžeme již dopočítat zdánlivý výkon (S) jednoho vinutí. To bude 400V x 17,4A = okolo 7 kVA. Opět vynásobíme zdánlivý výkon jednoho vinutí třemi a to bude 3 x 7 kVA = 20,9 kVA.
To je trojnásobný nárůst proudu v přívodních vodičích a také trojnásobný nárůst výkonu.

Při přepojení motoru z hvězdy (Y) do trojúhelníka (Δ) tedy musíme myslet i správně dimenzované vodiče a jistící prvky. Rázový proud při rozběhu do trojúhelníku by totiž byl opravdu velký a B32A jistič by ho zcela jistě neudržel, ačkoliv s hvězdou by problém neměl.
No a proto máme přepínače hvězda / trojúhelník (Y/0/Δ), které nám tyto silné motory pomáhají rozběhnout na třetinový proud do hvězdy (Y) a po roztočení se motor přepne na vyšší výkon do trojúhelníku (Δ). O tom více v tomto článku o přepíná motoru hvězda / trojúhelník.
Pro jistotu si ještě ukážeme odvození jednotlivých vzorců pro výpočet výkonu v třífázové soustavě.
V prvním příkladu jsme řešili zdánlivý výkon motoru pokud vodiči protéká stejný proud při stejném napětí. Měnil se jen způsob zapojení motoru a oba motory pak musely mít stejný výkon.
Co se týče Ohmova zákona, tak ze známé trojice proud, napětí, odpor (impedance) docházelo jen ke změně impedance vinutí.

V druhém příkladu jsme naopak řešili zdánlivý výkon motoru pokud se nemění napětí a impedance vinutí. Měnil se opět způsob zapojení motoru a oba motory měly rozdílný výkon, protože při zapojení do trojúhelníku protékal motorem trojnásobný proud.
Co se týče Ohmova zákona, tak ze známé trojice proud, napětí, odpor (impedance) docházelo jen ke změně protékajícího proudu.
Z níže uvedeného obrázku je zřejmé, že přepnutím z hvězdy do trojúhelníku, dojde k trojnásobnému nárůstu protékajícího proudu a tím i výkonu.

Máme motor s výkonem P = 8kW, účiníkem cosφ = 0,8 a účinností η = 80%, který je připojen do hvězdy na fázové napětí U = 230V. Jaký proud teče přívodními vodiči? Jak velká je jeho činná a jalová složka?
Nejprve musíme zjistit příkon motoru (Pp), který je odpovídá výkonu na hřídeli motoru povýšeného o účinnost. Čili Pp = P / η = 8kW / 0,8 = 10kW. Víme, že příkon motoru (Pp) odpovídá činnému výkonu (Pp).
Celkový odebíraný proud (Is) jednotlivými vinutími bude Pp / (3 x U x cosφ) = 10kW / (3 x 230 x 0,8) = 18,1A.
Činný proud (Ip) zjistíme vynásobením celkového proudu a účiníku cosφ = 18,1A x 0,8 = 14,5A
Jalový proud (Iq) zjistíme vynásobením celkového proudu (Is) a sinusem úhlu pro účiník cosφ = 18,1A x 0,6 = 10,9A
Zdánlivý výkon (Ps) zjistíme jako součet zdánlivých výkonů jednotlivých vinutí, které spočítáme jako součin napětí (U) a procházejícího proudu (Is). Ps = 3 x 230V x 18,1A = 12,5 kVA.
Činný výkon (Pp) zjistíme stejně jako zdánlivý výkon (Ps) vynásobený účiníkem cosφ. Pp = Ps x cosφ = 12,5 kVA x 0,8 = 10 kW. Činný výkon (Pp) bychom mohli i spočítat jako Pp = 3 x U x Ip = 3 x 230V x 14,5A = 10 kW.
Jalový výkon (Pq) zjistíme stejně jako zdánlivý výkon (Ps) vynásobený účiníkem sinφ. Pq = Ps x sinφ = 12,5 kVA x 0,6 = 7,5 kVar. Jalový výkon (Pq) můžeme zjistit i jako Pq = 3 x U x Iq = 3 x 230V x 10,9A = 7,5 kVar.
Máme ten samý motor jako v příkladu 1. Motor s výkonem P = 8kW, účiníkem cosφ = 0,8 a účinností η = 80%, který je připojen do trojúhelníku na fázové napětí U = 230V. Jaký proud teče přívodními vodiči? Jak velká je jeho činná a jalová složka?
Nejprve si musíme uvědomit, že napětí při zapojení do trojúhelníku je napětí sdružené a pokud máme v zásuvce fázové napětí 230V, tak do motoru půjde napětí sdružené ve výši Us = √3 x 230V = 400V.
Následně musíme zjistit příkon motoru (Pp), který je odpovídá výkonu na hřídeli motoru povýšeného o účinnost. Čili Pp = P / η = 8kW / 0,8 = 10kW. Víme, že příkon motoru (Pp) odpovídá činnému výkonu (Pp).
Fázový proud (If) jednotlivými vinutími bude Pp / (3 x Us x cosφ) = 10kW / (3 x 400 x 0,8) = 10,4A. Síťový proud pak zjistíme jako I = √3 x If = 18,1A.
Činný proud (Ip) zjistíme vynásobením celkového proudu a účiníku cosφ = 18,1A x 0,8 = 14,5A
Jalový proud (Iq) zjistíme vynásobením celkového proudu (Is) a sinusem úhlu pro účiník cosφ = 18,1A x 0,6 = 10,9A
Zdánlivý výkon (Ps) zjistíme jako součet zdánlivých výkonů jednotlivých vinutí, které spočítáme jako součin napětí (U) a procházejícího proudu (Is). Ps = 3 x Us x If = 3 x 400V x 10,4A = 12,5 kVA nebo jako Ps = √3 x Us x Is = √3 x 400V x 18,1A = 12,5kVA.
Činný výkon (Pp) zjistíme stejně jako zdánlivý výkon (Ps) vynásobený účiníkem cosφ. Pp = Ps x cosφ = 12,5 kVA x 0,8 = 10 kW. Činný výkon (Pp) bychom mohli i spočítat jako Pp = √3 x Us x Is x cosφ = √3 x 400V x 18,1A x 0,8 = 10 kW.
Jalový výkon (Pq) zjistíme stejně jako zdánlivý výkon (Ps) vynásobený účiníkem sinφ. Pq = Ps x sinφ = 12,5 kVA x 0,6 = 7,5 kVar. Jalový výkon (Pq) můžeme zjistit i jako Pq = √3 x Us x Is x sinφ = √3 x 400V x 18,1A x 0,6 = 7,5 kVar.
Všimněte si, že všechny proudy i výkony jsou při zapojení do hvězdy stejné jako při zapojení do trojúhelníku, protože přívodními vodiči teče v obou případech stejný proud při stejném napětí. Jak jsme už říkali výše... další energii si z prstu nevycucáme.
Jakou impedanci Z mají jednotlivá vinutí motoru, který má příkon Pp = 12kW, účiníkem cosφ = 0,8 a v síťovém napětí U = 230V zapojený do hvězdy?
Abychom mohli spočítat impedanci, musíme zjistit celkový síťový proud (Is), který protéká jednotlivými vinutími. Is = Pp / (3 x U x cosφ) = 12kW / (3 x 230 x 0,8) = 21,7A.
Impedanci vinutí zjistíme podle Ohmova zákona jako Z = U / Is = 230V / 21,7A = 10,6Ω.
Pro kontrolu spočítáme výkon. Pp = 3 x U x Is x cosφ, kde U = Is x Z. Potom Pp = 3 x (21,7A x 10,6Ω) x 21,7A x 0,8 = 12 kW.
Jakou impedanci Z mají jednotlivá vinutí motoru z příkladu 3, který má příkon Pp = 12kW, účiníkem cosφ = 0,8 a v síťovém napětí U = 230V zapojený do trojúhleníku?
Opět nejprve zjistíme sdružené napětí Us = Uf x √3 = 230V x √3 = 400V. Abychom mohli spočítat impedanci, musíme zjistit fázový proud (If), který protéká jednotlivými vinutími. If = Pp / (3 x Us x cosφ) = 12kW / (3 x 400 x 0,8) = 12,5A.
Impedanci vinutí zjistíme podle Ohmova zákona jako Z = U / Is = 400V / 12,5A = 32Ω.
Pro kontrolu spočítáme výkon. Pp = 3 x U x Is x cosφ, kde U = Is x Z. Potom Pp = 3 x (12,5A x 32Ω) x 12,5A x 0,8 = 12 kW.
Jaký zdánlivý, činný a jalový výkon by měl motor z příkladu 4, pokud by měl impedanci vinutí jako motor z příkladu 3? Čili jaký zdánlivý, činný a jalový výkon by měl motor zapojený do trojúhelníku, s účiníkem cosφ = 0,8 při síťovém napětí U = 230V a impedancí vinutí Z = 10,6Ω?
Opět nejprve zjistíme sdružené napětí Us = Uf x √3 = 230V x √3 = 400V. Fázový proud (If), který protéká jednotlivými vinutími zjistíme jako If = Us / Z = 400V / 10,6Ω = 37,8A.
Zdánlivý výkon Ps = 3 x U x Is, kde U = Is x Z. Potom Pp = 3 x (37,8A x 10,6Ω) x 37,8A = 45,4 kVA.
Činný výkon Pp = 3 x U x Is x cosφ, kde U = Is x Z. Potom Pp = 3 x (37,8A x 10,6Ω) x 37,8A x 0,8 = 36,3 kW.
Jalový výkon Pq = 3 x U x Is x sinφ, kde U = Is x Z. Potom Pp = 3 x (37,8A x 10,6Ω) x 37,8A x 0,6 = 27,2 kVar.
Všimněte si, že motor v tomto příkladu má 3x větší výkon a proud než motor v příkladu 3, ačkoliv mají stejnou impedanci vinutí. To jsme si již vysvětlili výše... Výkon motoru zapojeného do trojúhelníku je při stejném síťovém napětí a impedanci vinutí třikrát větší než motor zapojený do hvězdy.
V přívodním vedení do třífázového sporáku nebo bojleru připojeného do běžné domácí sítě byl naměřen proud Is = 16A. Zapojení spotřebiče je do trojúhelníku. Jak velký proud prochází jednou topnou spirálou? Jak velký je odpor spirály (Z) a jak velký příkon (Pp) spotřebič se třemi spirálami má?
Opět si ujasníme napětí. Spotřebič je zapojen do běžné sítě, ve které je fázové napětí 230V. Protože spotřebič je zapojen do trojúhelníku, musíme fázové napětí upravit na napětí sdružené Us = Uf x √3 = 230V x √3 = 400V. Účiník cosφ u tepelných spotřebičů můžeme počítat jako 1.
Fázový proud If procházející jednou spirálou bude If = Is / √3 = 16A / √3 = 9,2A.
Odpor spirály pak určíme pomocí Ohmova zákona jako Z = Us / If = 43,3Ω.
Celkový příkon (Pp) sporáku popř. bojleru pak určíme jako Pp = 3 x Us x If x cosφ = 3 x 400V x 9,2A x 1 =11 kW.
Stejný výsledek pochopitelně dostaname i při použití vztahu Pp = √3 x Us x Is x x cosφ = √3 x 400V x 16A x 1 = 11 kW.
Co kdybychom ten samý spotřebič z příkladu 6 zapojili do hvězdy? Jakou impedanci jedna spirála bude mít? Jaký bude příkon sporáku / bojleru?
Je to vlastně pořád dokola. Již bezpečně víme, že pokud se nezměnil proud ani napětí, nemůže dojít ke změně příkonu spotřebiče. Takže sporák nebo bojler mají příkon 11 kW.
Jedinou proměnou je tedy impedance spirály, kterou prochází fázový proud If = 16A při napětí 230V. Z = Uf / If = 230V / 16A = 14,4Ω.
Pro kontrolu si to celé ještě ověřmě výpočtem příkonu Pp.
Celkový příkon (Pp) sporáku popř. bojleru pak určíme jako Pp = 3 x Uf x If x cosφ = 3 x 230V x 16A x 1 =11 kW.
Stejný výsledek pochopitelně dostaname i při použití vztahu Pp = √3 x Us x Is x x cosφ = √3 x 400V x 16A x 1 = 11 kW.
Zkusme si představit sporát nebo bojler z příkladu 7, čili spotřebič který je zapojený do hvězdy, vodiči protéká proud 16A při fázovém napětí 230V. Jaký bude výkon spotřebiče pokud dojde k přehoření jedné tepelné spirály/patrony?
V tomto příkladu si musíme uvědomit, jak je zapojení do hvězdy provedeno. Jestli je provedeno s nulovým vodičem nebo bez, protože nyní to má na výpočet vliv.
Pokud bychom uvažovali zapojení do hvězdy s nulovým vodičem, potom přehoření jedné spirály povede k poklesu výkonu o jednu třetinu. Proud ze zbylých dvou fází se může vracet právě nulovým vodičem. Je to vlastně jako bychom měli tři jednofázové rychlovarné konvice vedle sebe a jedna se rozbila.
Výkon bychom pak počítali jako Pp = 2 x Uf x If x cosφ = 2 x 230V x 16A x 1 = 7,36 kW. Viz obrázek niže.
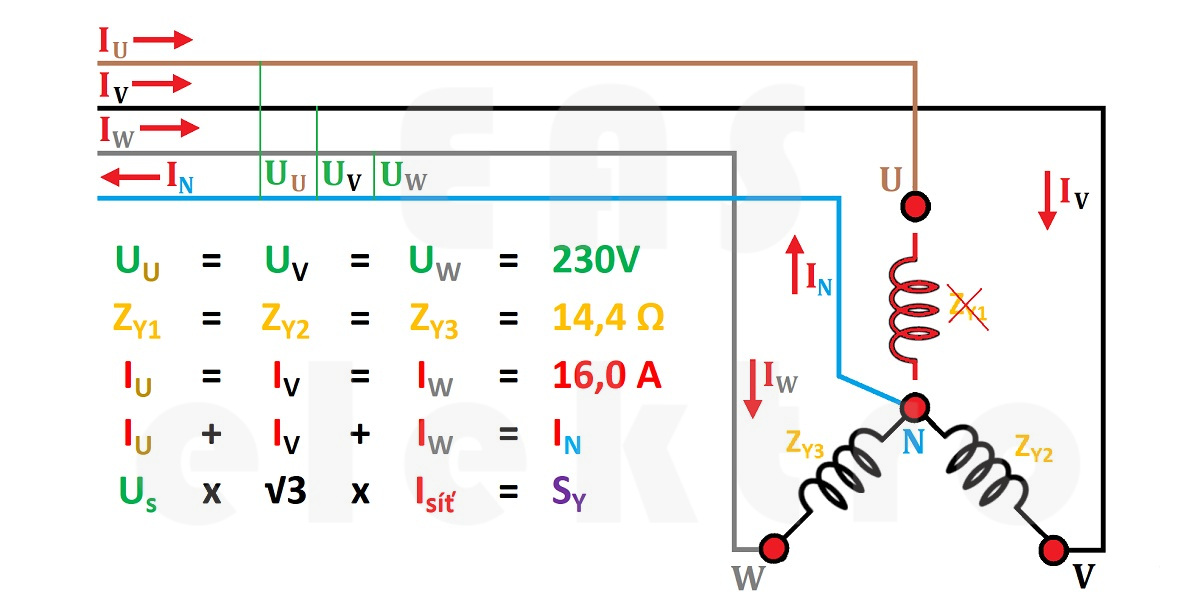
Pokud bychom uvažovali zapojení do hvězdy bez nulovoho vodiče, nelze to počítat už tak jednoduše. Zde si třeba uvědomit, že proud se vrací zpátky fázovým vodičem. Dalo by se vlastně i říct, že se z třífázového spotřebiče stal spotřebič jednofázový, fungující nikoliv na síťové napětí, ale na napětí sdružené. Viz obrázek niže.
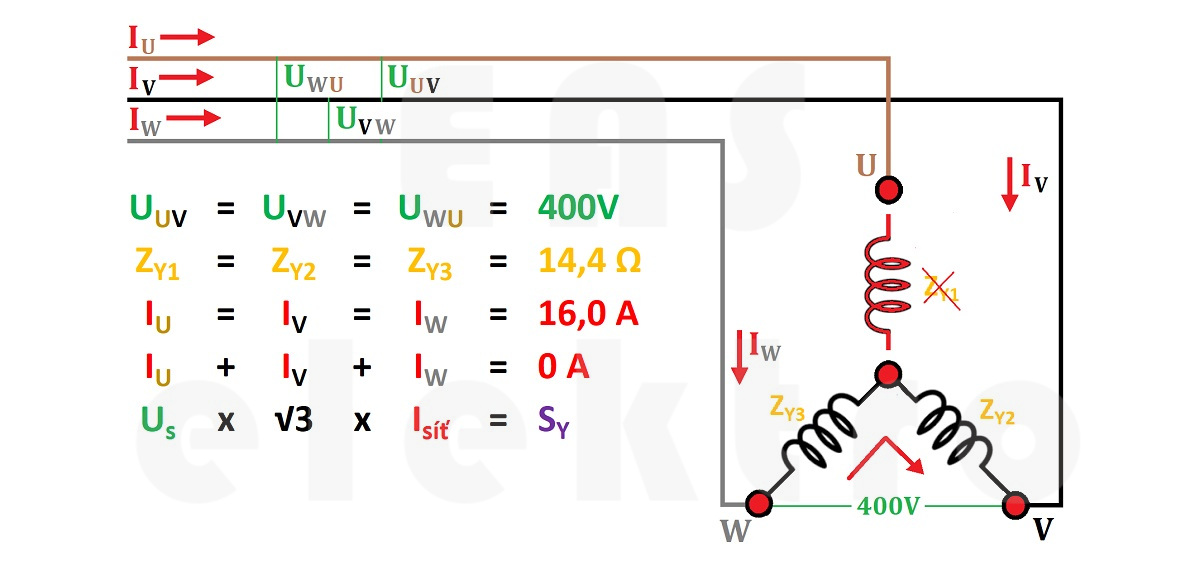
Při přepálení spirály se proud již nemůže vracet touto poškozenou větví. Impedanci spirál již známe z předchozích příkladů Z = 14,4Ω, stejně jako sdružené napětí. Nyní nám stačí jen zjistit protékající proud, ale nesmíme zapomenout, že sdruženému napětí 400V kladou nyní překážky obě spirály... I = Us / Zy2 + Zy3 = 400V / (14,4Ω + 14,4Ω) = 13,9 A.
Výkon bychom pak počítali jako Pp = U x I x cosφ = 400V x 13,9A x 1 = 5,55 kW.
Z výpočtu je zřejmé, že výkon sporáku zapojeného do hvězdy klesl více při zapojení bez nulového vodiče než při zapojení s nulovým vodičem.
Pokud by došlo k vyhoření dvou spirál, tak v případě zapojení do hvězdy s nulovým vodičem by sporák fungoval alespoň z jedné třetiny. V případě zapojení sporáku do hvězdy bez nulového vodiče, by sporák nefungoval vůbec, protože by nebyl uzavřený obvod.
Pokud jste v článku nalezli chybu, dejte nám, prosíme, o ní vědět na eas@eas-elektro.cz
Děkujeme, Eva a Aleš Smetákovi - návrat zpět na přehled článků