15.10.2023 - Ing. Aleš Smeták
Pro vysvětlení Ohmova zákona je asi nejlepší používat oblíbenou vodní analogii, protože elektrický proud se v tomto případě chová dost podobně jako voda v hadici a tu si na rozdíl od elektrického proudu umíme hravě představit.
Představte si, že elektrický proud je jako protékající voda v zahradní hadici a že elektrické napětí je jako tlak vody z vodárny. A odpor? K tomu se dostaneme průběžně.
No a teď si ještě představme, že zmíněnou hadicí máme za úkol napustit venkovní bazének. Všichni jsme se s tím už setkali. Pokud se v poledne rozhodneme, že se chceme po obědě vykoupat, tak máme smůlu... hadice prostě potřebuje nějaký čas, aby bazének naplnila.
Asi se shodneme, že pokud chceme napustit bazének rychleji, musíme nějak zvětšit objem protékající vody hadicí. Ale jak? Toho lze v zásadě dosáhnout dvěma způsoby:
A kde je pořád ten odpor? No přiznám se, že tady už půjdu se zjednodušováním fakt na hranu a zkušený elektrotechnik by se při dalším čtení měl posadit. Vlastně proč by tohle vůbec měl číst zkušený elektrotechnik?
No nic, zpátky k věci. Proč se zvětšením průřezu hadice zvýší i průtok? Protože klesne odpor, který hadice proudící vodě klade. Jednoduché říci, složitější ovšem pochopit.
Ačkoliv se to nezdá, tak voda v hadici neteče rovnoměrně, ale nejsnadněji se jí teče uprostřed průřezu hadice, a naopak nejvíc se nadře u krajů při dotyku s pláštěm hadice. Tomu se říká turbulentní proudění, ale to už je fakt nad rámec.
Zvětšením průřezu tak sice roste obvod hadice, ale i zároveň i její průřez... ten ovšem roste mnohem rychleji než obvod a vodě se tak prostě nějak teče lépe.
Tohle ovšem neplatí jen u průřezu hadice, ale i u její délky. Určitě jste si všimli, že metrovou hadicí teče voda mnohem snáze než stometrovou a že u dlouhých řadů musí být přečerpávací stanice.
Prakticky si to můžete vyzkoušet s obyčejným brčkem. Schválně zkuste dýchat přes jedno brčko a pak si spojte tři brčka za sebe a zkuste to nyní. To, co vás začne spolehlivě dusit, je...
A to je právě ten odpor, který závisí na průřezu hadice, její délce, ale i počtu uzlů, kolínek nebo dalších překážek, které vodě nějak komplikují cestu. U elektřiny to funguje naprosto stejně.

Elektrické napětí si můžeme představit jako neviditelnou sílu, která se snaží protlačit elektrický proud skrze vodič a odpor je taková zákeřná mrška, která ji v tom brání.
Z tohoto důvodu se pro výrobu vodičů používají materiály, které mají co nejnižší odpor. Například měď nebo hliník. Ačkoliv jsou i materiály s nižší odporem, jejich využití nedává ekonomický smysl.
Pokud by odpor neexistoval, respektive byl nulový, mohlo by napětí protlačit jakékoliv množství proudu s naprosto minimální silou. To by byl ideální stav a takovému vodiči by se pak říkalo supravodič.
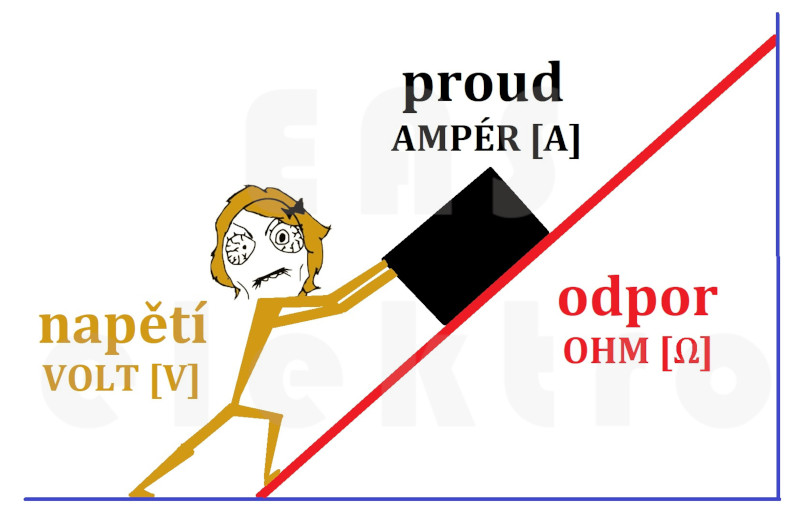
Čím větší odpor je, tím větší sílu napětí musí vyvinout, aby proud elektronů skrze vodič protlačilo. Pokud by nějaká látka měla elektrický odpor silnější než napětí, potom by napětí žádný proud skrze tuto látku neprotlačilo a látka by fungovala jako izolant.
Jenže... žádná látka nemá nekonečný odpor a pokud napětí poroste do závratných výšin, najde si cestu i skrze látku s vysokým odporem. Pokud si tedy do prodlužky pustíte 230V, odpor izolace vodičů toto napětí podrží na uzdě, ale pokud byste do běžné domácí prodlužky nějak dostali vysoké napětí... její izolace vás neochrání.
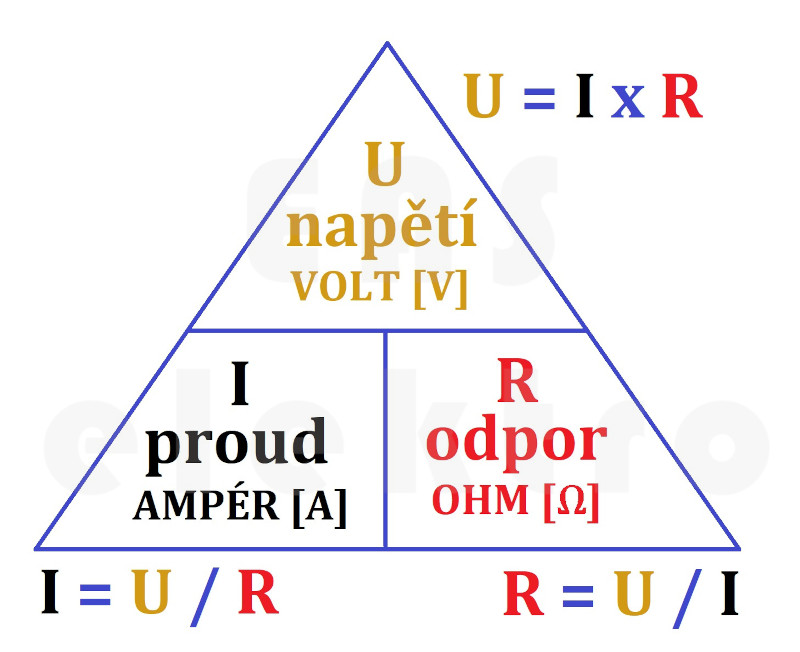
Napětí, odpor a proud jdou neustále ruku v ruce a jeden bez druhého by neexistovaly. Ukážeme si to na několika jednoduchých příkladech:
Kirchhoffovy zákony nám umožňují pochopit, jak se elektrická energie (proud a napětí) chová v uzavřených obvodech.
Součet všech proudů přitékajících do uzlu je v každém okamžiku roven součtu proudů z uzlu vytékajících.
Jinak řečeno, algebraický součet proudů v uzlu je roven nule.
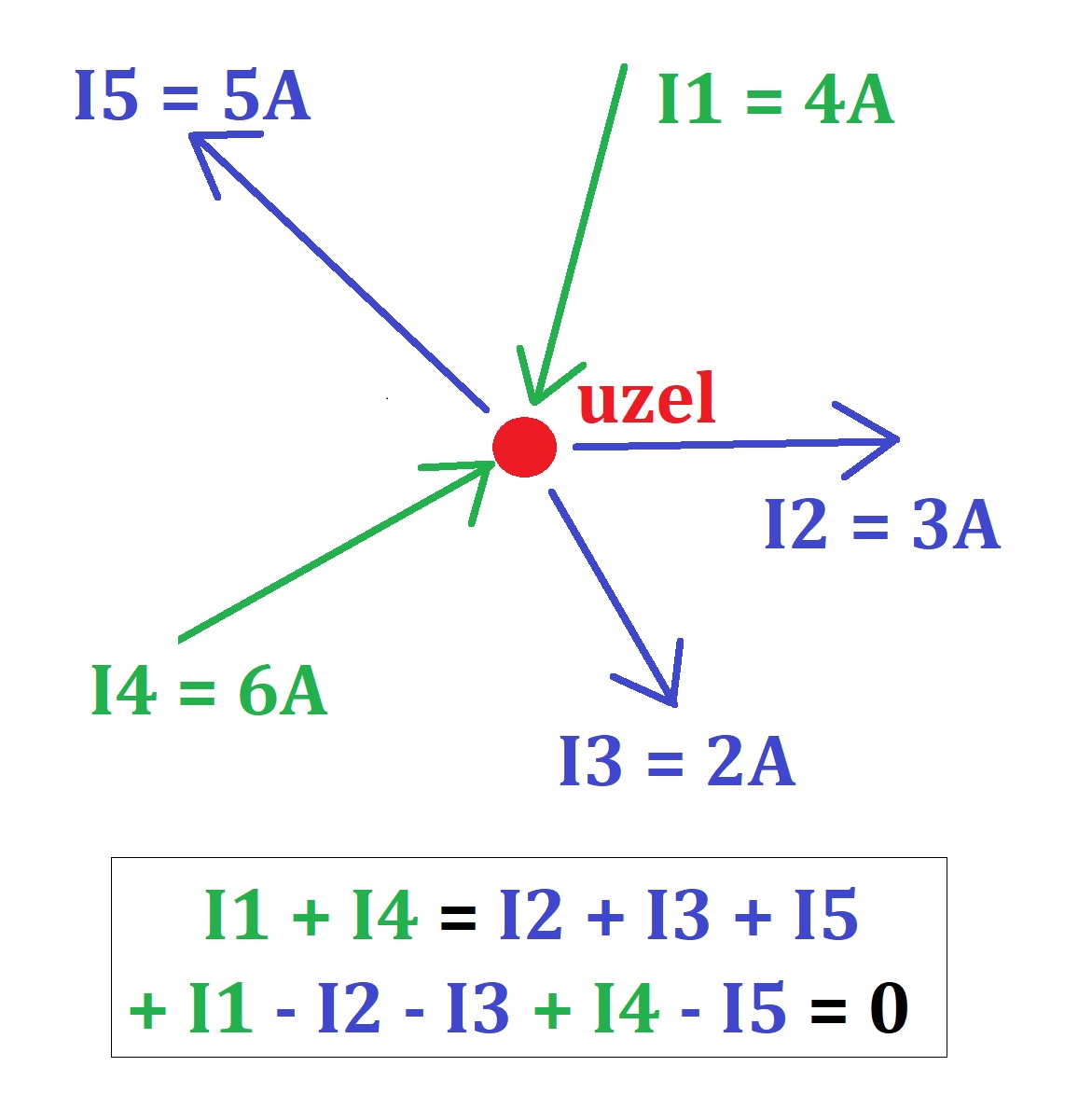
První Kirchhoffův zákon se týká proudu. Říká nám, že když máme uzavřený elektrický okruh, všechny proudy, které do něj vstupují, musí někam odejít. Jinými slovy, to, co jde do obvodu, musí také z obvodu ven.
Ve vodní analogii by se to dalo přirovnat k situaci, kdy chceme udržet konstantní hladinu v nádrži. Součet všech přítoků do nádrže musí být logicky stejný jako součet všech odtoků.
V uzavřené smyčce je součet napětí na rezistorech stejný jako součet napětí na zdrojích.
Jinak řečeno, algebraický součet napětí ve smyčce je roven nule.
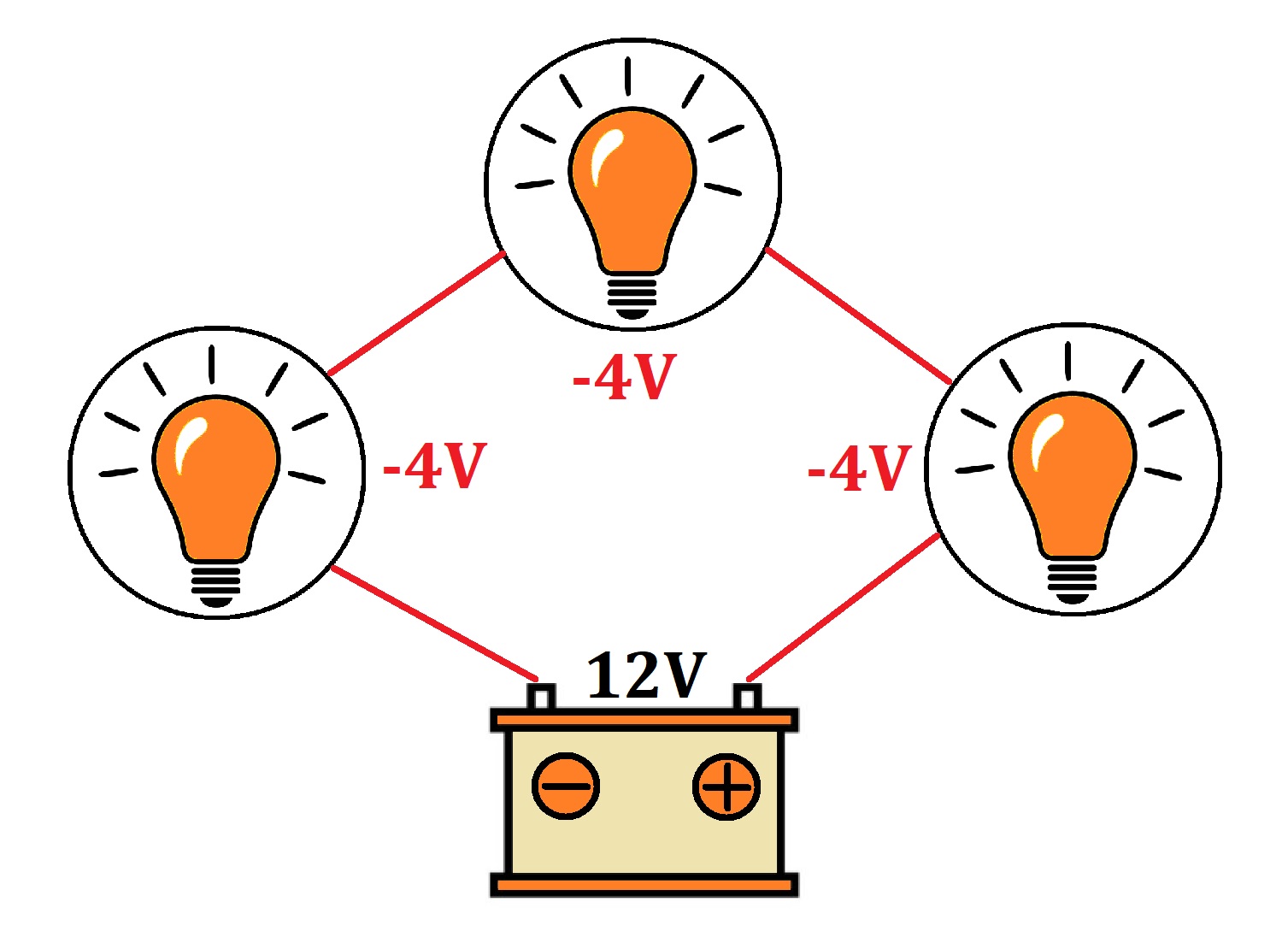
Druhý Kirchhoffův zákon se týká napětí. Když jdeme v elektrickém obvodu po kruhu, tak součet všech zdrojů napětí musí být roven součtu všech „spotřebičů“ napětí.
Ve vodní analogii by se to dalo přirovnat k situaci, kdy opět chceme udržet konstantní hladinu v nádrži, do které přitéká voda jednou trubkou a odtéká dvěma. Pokud bychom chtěli udržet konstantní hladinu v nádrži, tlak na přítoku musí být dvojnásobný než na odtoku.
Aplikaci Ohmova a Kirchhoffových zákonů si můžeme ukázat na následujícím příkladu, na který jsem narazil v jedné elektrikářské skupině a který se mi pro svoji jednoduchost a zároveň věcnost velmi zalíbil.
V zadání máme jasně definované hodnoty obvodu, kdy známe dva procházející proudy, jedno napětí a rovnost dvou odporů. To je bezpochyby dost informací k tomu, abychom mohli dopočítat všechny proudy procházející jednotlivými rezistory, úbytky napětí a ztrátové výkony na nich.
V prvním kroku jsem si zadání překreslil do barevného schématu, se kterým rád pracuji a které mi přijde přehlednější.

Nyní můžeme začít odvozovat jednotlivé hodnoty.
Nejjednodušší bude začít s výpočtem proudu I1, protože na základě prvního Kirchhoffova zákona víme, že součet proudů I1 a I2 se musí rovnat celkovému proudu. Odtud tedy I1 = I - I2 = 1,2A - 0,2A = 1A.
V dalším kroku zjistíme velikost jednotlivých odporů. Na základě Ohmova zákona víme, že odpor R je podíl napětí U a proudu I. Protože již známe proudy I1 a I2 a také známe napětí U1, je snadné dopočítat odpory R1 a R2. Odtud tedy R1 = 12Ω a R2 = 60Ω. Ze zadání víme, že odpor R3 je stejný jako R1, a proto R3 = 12Ω.
Dále dopočítáme úbytky napětí. Úbytek napětí U1 známe již ze zadání a k výpočtu úbytku napětí U2 opět využijeme Ohmova zákona, který říká, že napětí U je součin odporu R a proudu I. Proud i odpor známe z předchozích kroků a odtud tedy U2 = 1,2A x 12Ω = 14,4V.
Celkový úbytek napětí je roven napětí, které musí zdroj poskytnout. Celkový úbytek napětí (napětí zdroje) zjistíme na základě druhého Kirchhoffova zákona. Odtud tedy U = U1 + U2 = 12V + 14,4V = 26,4V.

Jako poslední zjistíme ztrátový výkon na jednotlivých odporech (rezistorech). V tomto případě Ohmova ani Kirchhoffových zákonů nevyužijeme. Výkon P se totiž počítá jako součin napětí U a proudu I.
Procházející proudy a úbytky napětí již známe. Odtud tedy P1 = U1 x I1 = 12V x 1A = 12W a stejným způsobem zjistíme ztrátové výkony i u ostatních rezistorů.
Podobné příklady na sériové a paralelní obvody s rezistory naleznete v samostatném článku.
Pokud jste v článku nalezli chybu, dejte nám, prosíme, o ní vědět na eas@eas-elektro.cz
Děkujeme, Eva a Aleš Smetákovi - návrat zpět na přehled článků