31.3.2024 - Ing. Aleš Smeták
V tomto článku se podíváme na zoubek elektrickému výkonu a příkonu v jednofázové soustavě. Budeme se zabývat výkonem v jednofázové soustavě a také si něco řekneme o rozdílech výkonu v případě střídavého a stejnosměrného napětí/proudu. Výkonem v třífázové soustavě se naopak zabývá tento článek.
Nejprve si však zopakujeme základní fyzikální pojmy, abychom vůbec věděli, o čem se bavíme.
Na základní škole jsme se všichni učili o základních fyzikalních veličinách jako jsou práce (W), výkon (P) a příkon (Pp), které se nyní pro jistotu zopakujeme.
Práce v fyzice není něco, co bychom dělali na staveništi nebo v kanceláři. Ve fyzice je práce speciální termín, který nám pomáhá porozumět, jak síly ovlivňují pohyb předmětů.
Představte si, že máte sešívačku, která leží na stole. Když ji posuneme směrem k oknu, uděláme práci. Proč? Protože musíme překonat tření mezi sešívačkou a stolem, abychom ji posunuli. Tím, že posouváme sešívačku, přenášíme energii ze svých svalů na sešívačku, a to je právě ta práce. Vzorec k výpočtu práce vypadá takto:
práce (W) = síla (F) × vzdálenost (s) × kosinus úhlu (α) mezi silou a směrem pohybu
1 J = 1 N x 1m x cos0°
Teď to může znít trochu složitě, ale zkusme to zjednodušit. Když posouváme sešívačku, síla, kterou používáme, je ta, kterou vynakládáme svými svaly. Vzdáleností je vzdálenost, kterou sešívačku posouváme. A kosinus úhlu je trochu složitější, ale můžeme si ho představit jako úhel mezi směrem, kterým táhneme sešívačku, a směrem, kterým se sešívačka skutečně pohybuje.
Celkově vzato, práce nám pomáhá pochopit, jak síly ovlivňují pohyb věcí. Čím větší sílu vynaložíme nebo čím delší trasu překonáme, tím více práce vykonáme. Takže, práce je:
Představme si benchpressovou činku o váze 150kg, kterou zvedneme na délku paží 60 cm. Jakou práci vykonáme?
Dosadíme do vzorce W = F x s x α = 1500N x 0,6m x 1 a zjistíme, že jsme vykonali práci 900J.
Výkon v podstatě popisuje, jak rychle nebo pomalu děláme PRÁCI (W). Když děláme práci rychle, máme vysoký výkon, a když ji naopak děláme pomalu, máme malý výkon. Představme dvě situace:
Sprinter - Když běžec běží velmi rychle, má vysoký výkon, protože rychle překonává vzdálenost.
Jogger - Když běžec pomalu kráčí, má nižší výkon, protože pohyb probíhá pomaleji.
Výkon se měří ve wattech. Čím více watů, tím vyšší výkon k výpočtu výkonu použijeme vzorec:
výkon (P) = práce (W) / čas (t)
1 W = 1 J / 1s
1 J = 1 W x 1s
To znamená, že výkon je poměr mezi práci, kterou děláme, a časem, za který ji vykonáme a výkon jednoho wattu odpovídá vykonané práci 1 joule za 1 sekundu.
Pokračujme v předchozím příkladu s benchpressovou činkou... pokud bychom tuto činku zvedli za 1 vteřinu, tak výkon bude P = W / t = 900J / 1s = 900W. Pokud bychom tu samou činku zvedali 3 vteřiny, byl by výkon 900J / 3s = 300W.
Příkon je trochu jiný než výkon. Příkon se týká energie, kterou vkládáme do zařízení a příkon si můžeme představit jako to, kolik energie potřebujeme do zařízení dodat, aby správně fungovalo.
Čím více energie zařízení k provozu spotřebovává, tím vyšší příkon potřebuje. Příkon se měří ve wattech, stejně jako výkon a pro jeho výpočet se používá vzorec:
příkon (Pp) = e
nergie (E)
/ čas
(t)
1 W = 1J / 1s
Opět budeme pokračovat v předchozím příkladu a abychom si to prozatím zjednodušili, budeme uvažovat, že výkon motoru je stejný jako příkon. To pochopitelně není pravda, protože účinnosti 100% nelze dosáhnout.
Už víme, že abychom činku zvedli, musíme vykonat práci (W) čili dodat energii (E) ve výši 900J. Pokud bychom činku chtěli zvednout motorem za 9 vteřin, tak dosadíme do vzorečku Pp = E / t = 900J / 9s = 100W. Tedy aby motor činku pomocí převodů zvedl za 9 vteřin, musí mít příkon/výkon 100W. Pokud bychom chtěli, aby motor činku zvedl za poloviční čas, museli bychom příkon/výkon zdvojnásobit.
Účinnost (η) je poměr mezi výkonem (P) a příkonem (Pp) a uvádí se v procentech. Je logické, že účinnost nemůže být vyšší než 100%, protože by množství vykonané práce bylo vyšší než množství dodané energie a tomu pak říkáme perpetuum mobile.
účinnost (η) = výkon (P) / příkon (Pp)
Pokud budeme mít motor, který na hřídeli dodává výkon 100W a spotřebovává příkon 125W, tak jeho účinnost bude 80%. Rozdíl mezi příkonem (Pp) a výkonem (P) se označuje jako "ztráty".
Účiník (cos φ) je poměr mezi skutečným výkonem (užitečným výkonem) a zdánlivým výkonem ve spotřebiči. V případě elektromotoru můžeme si účiník představit jako to, jak efektivně se elektrická energie, kterou dodáváme motoru, přeměňuje na mechanickou energii motoru, která pohání nějaký stroj nebo zařízení.
Pokud má elektromotor vysoký účiník, znamená to, že většina elektrické energie se efektivně využívá k pohonu motoru. Naopak, pokud má nízký účiník, část energie se může ztrácet ve formě tepla nebo jiných nežádoucích jevů, což znamená, že motor není tak efektivní.
Účiník se obvykle vyjadřuje jako číslo mezi 0 a 1. Čím blíže k 1, tím efektivněji motor pracuje. Účiník je vlastně poměr mezi výkonem elektromotoru (P) a jeho skutečně potřebném příkonu (Pp).
V naprosto ideální podmínkách bez jakýchkoliv nežádoucích ztrát by byl účiník 1, ale je prakticky nedosažitelná meta. V opačném případě by byl účiník 0 a motor by veškerou dodanou energii spotřeboval jen na vlastní provoz.
S účiníkem souvisí i pojmy jako je zdánlivý výkon, činný výkon a jalový výkon.
Zdánlivý výkon (S) = napětí (U) x proud (I) - zdánlivý výkon je prostý součin proudu a napětí a uvádí se voltampérách (VA).
Činný výkon (P) - napětí (U) x proud (I) x
cos
φ - č
inný výkon vyjadřuje energii, která se v motoru skutečně přemění na mechanickou energii a uvádí se ve wattech (W).
Jalový výkon (Q) - napětí (U) x proud (I) x sin
φ - jalový výkon vyjadřuje energii, která se přelévá
mezi zdrojem a spotřebičem tam a zpět a uvádí se ve voltampérech reaktančních (var).
Zdánlivý, potažmo celkový výkon (S), lze také spočítat jako součet činného výkonu (P) a jalového výkonu (Q) podle vzorce:
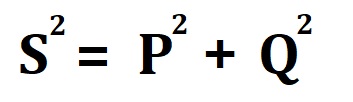
Účinnost (η) a účiník (cos φ) jsou oba ukazatele efektivity elektrických systémů, ale míří na různé aspekty a nesmíme si je proto
plést
.
Účinnost (η) se zaměřuje na to, jak dobře systém přeměňuje vstupní energii na užitečnou výstupní energii.
Účiník (cos
φ
)
měří poměr mezi činným výkonem a zdánlivým výkonem v elektrických obvodech.
Pokud má systém vysoký účiník (cos φ), znamená to, že poměr mezi činným (P) a zdánlivým (S) výkonem je vysoký, což může indikovat efektivní využití energie. To může vést k vyšší účinnosti systému, pokud je zachována konstantní úroveň výstupního výkonu.
Nicméně, účiník (cos φ) sám o sobě není přímým ukazatelem účinnosti (η)
, protože účinnost (η) měří skutečný poměr mezi vstupní a výstupní energií, zatímco účiník (cos φ) se zaměřuje na poměr mezi činným a zdánlivým výkonem.
Pro výpočet elektrického příkonu můžeme využít následující vzoreček:
příkon (Pp) = napětí (U) x proud (I)
Zkusme dále rozvíjet náš příklad s činkou. Už víme, že při výkonu motoru 100W potřebujeme příkon 125W, protože účinnost motoru je 80%. Jaký proud budeme potřebovat, aby nám motor činku zvedl za předpokladu, že máme napětí 230V? Z výše uvedeného vzorce lze snadno extrahovat proud I = Pp / U = 125W / 230V = 0,54A. Nyní víme, že vodiči k motoru poteče proud ve výši zanedbatelných 0,54A.
Pokud bychom činku chtěli hypoteticky zvednout za desetinu vteřinu, potřebovali bychom výkon 9.000W a příkon asi 9.000W / 80% = 11.250W. Potřebný proud pak bude I = 11.250W / 230V = 48,9A, což už by byl proud, na který není domácí rozvod dimenzovaný.
Nyní si příklad malinko zkomplikujeme tím, že do něj vložíme již zmíněný účiník (cos φ).
činný výkon (P) = napětí (U) x proud (I) x cos φ
Stejně jako v předchozím příkladu. Jaký proud budeme potřebovat, aby nám motor s činným výkonem 100W zvedl činku za předpokladu, že máme napětí 230V a účiník (cos φ) = 0,9?
Z výše uvedeného vzorce lze snadno extrahovat proud I = P / (U x cos φ) = 100W / (230V x 0,9) = 0,48A. Nyní víme, že vodiči k motoru poteče činný proud ve výši 0,48A.
Zkusme si ještě jeden příklad.
Jaký činný/jalový a zdánlivý výkon a proud má motor s účiníkem 0,65, kterým při napětí 230V protéká proud 10A?
Pokud se účiník cos φ = 0,65, tak φ musí být 49,46° a z toho sin φ = 0,76.
Zdánlivý výkon zjistíme snadno jako S = U x I = 230V x 10A = 2,300kW.
Činný výkon zjistíme jako P = U x I x cos(φ) = 230V x 10A x 0,65 = 1,495kW.
Z výše uvedených informací již můžeme dopočítat i jalový výkon, jehož druhá mocnina je rovna rozdílu druhých mocnin zdánlivého a činného výkonu. Tedy 2,300^2 - 1,495^2 =
3,054975^(1/2) = 1,748 var.
Pro kontrolu ještě zkusíme výpočet jalového výkonu jako Q = U x I x sin(φ) = 230V x 10A x 0,76 = 1,748 var.
Obdobně bychom se mohli dopočítat jednotlivých složek celkového proudu 10A.
Činný proud bude 1,495kW / 230V = 6,5A a jalový proud bude 1,748 / 230V = 7,6A.
Pokud bychom druhé mocniny obou složek proudu sečetli, tak 6,5A^2 + 7,6A^2 = 42,25A + 57,76A = 100A a to je opět druhá mocnina celkového proudu 10A.
Pokud jste v článku nalezli chybu, dejte nám, prosíme, o ní vědět na eas@eas-elektro.cz
Děkujeme, Eva a Aleš Smetákovi - návrat zpět na přehled článků