12.11.2023 - Ing. Aleš Smeták
V elektronických obvodech se setkáváme s nejrůznějšími prvky, z nichž rezistory hrají klíčovou roli v řízení velikosti proudu a napětí. Při návrhu a montáži elektronických obvodů je důležité správné řazení rezistorů (odporů), což může ovlivnit výsledné vlastnosti a chování celého systému.
Existují dva základní přístupy k řazení rezistorů - sériové a paralelní zapojení. Každý z těchto typů přináší specifické výhody a výzvy, a pochopení jejich rozdílů je klíčové pro efektivní návrh a optimalizaci elektronických obvodů.
V tomto článku se zaměříme na tyto dva způsoby řazení rezistorů, prozkoumáme jejich charakteristiky a nakonec si ukážeme komplexní příklad na kombinaci sériových a paralelních řazení odporů (rezistorů), ve kterém budeme zkoumat jednotlivé odpory, procházející proudy i úbytky napětí.
Snad nejjednodušším řazením rezistorů je sériové řazení - čili řazení za sebou - ve kterém se odpory prostě jen sčítají.
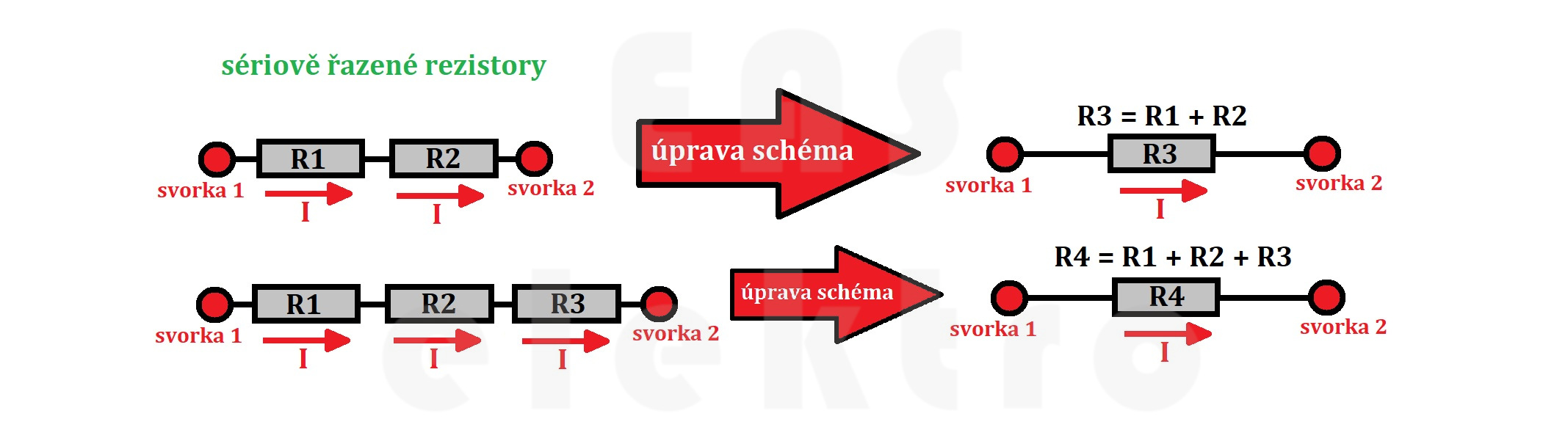
V sériovém schématu prochází stejný proud všemi rezistory a úbytek napětí je závislý na velikosti jednotlivých rezistorů v obvodu.
Obecně lze říci, že přidáním dalšího rezistoru do obvodu se sériovým řazením, se zvýší celkový odpor obvodu.
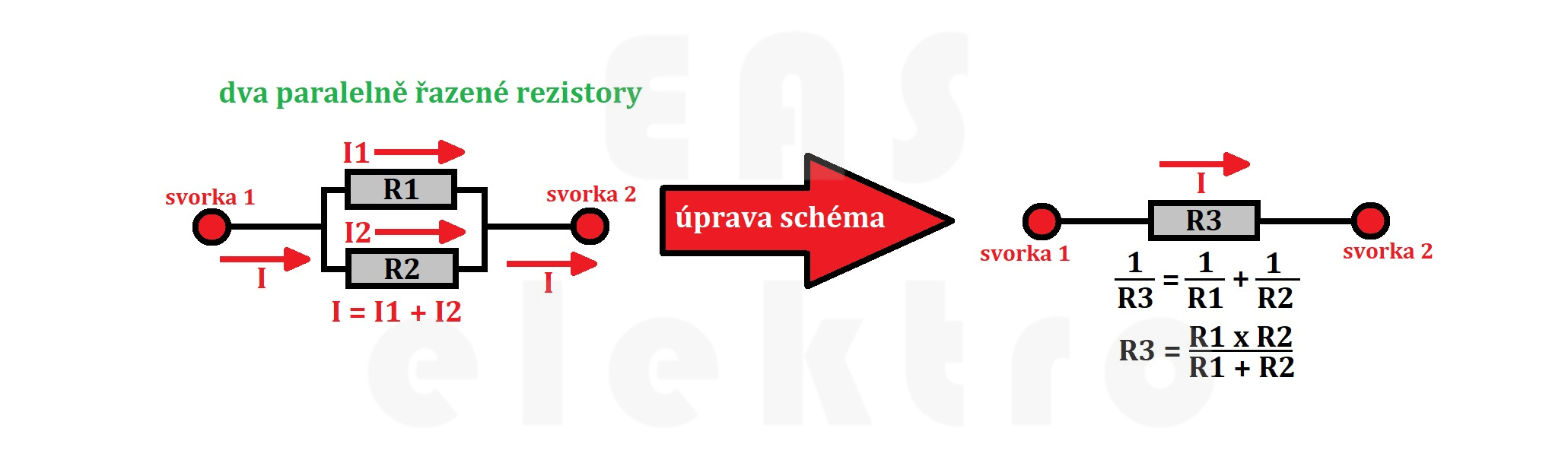
Opakem sériového řazení rezistorů je řazení paralelní, kdy rezistory jsou řazeny vedle sebe. Součet proudů procházející jednotlivými rezistory je celkový proud procházející obvodem.
Elektrický proud, který v paralelním řazením prochází jednotlivými rezistory, je také nepřímo úměrný jejich odporům. Jinak řečeno, čím větší odpor rezistor má, tím méně proudu jím prochází. Pokud mají oba rezistory stejný odpor, bude jimi procházet i stejný proud.
Obvod s dvěma paralelně řazenými rezistory lze zjednodušit jedním náhradním odporem, jehož velikost zjistíme podle následujícího vzorce.
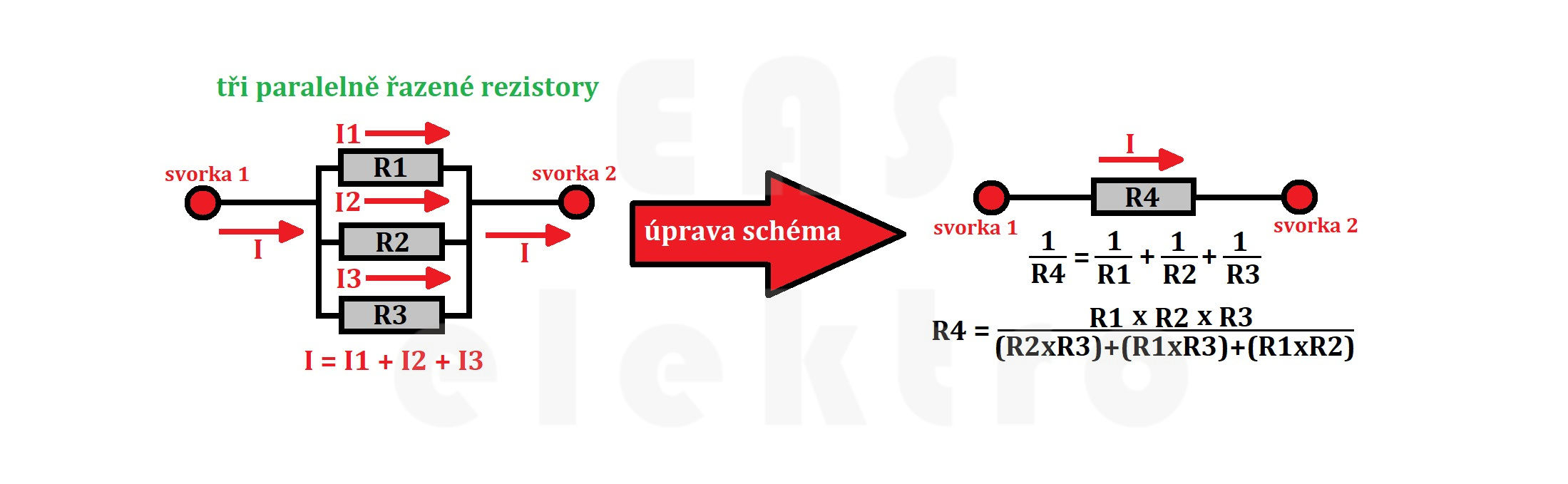
Úplně stejně platí i pro paralelní řazení třech odporů. Opět součet jednotlivých proudů odpovídá celkovému proudu procházejícím obvodem a pouze vzoreček pro výpočet je trochu složitější.
I v případě třech paralelních odporů můžeme obvod zjednodušit na jeden odpor.
No a když můžeme zjednodušit schéma s třemi paralelními rezistory, můžeme zjednodušit jakékoliv schéma bez ohledu na množství paralelních rezistorů.

Obecně platí, že čím více paralelních rezistorů je v obvodu, tím menší celkový odpor obvod má. Tohoto jevu se běžně využívá u dimenzování vodičů, protože zvětšení průřezu vodiče není vlastně nic jiného než přidání dalšího paralalního odporu.
Obdobně funguje i zemní odpor, protože ačkoliv zemina není dobrým vodičem, tak proud skrze ní prochází skvěle, protože má de facto nekonečný průřez... čili nekonečné množství paralelně řazených odporů.
Zvláštním případem jsou schémata, kde se vyskytují zároveň paralelně i sériově řazené rezistory.
Taková schémata lze upravit postupným zjednodušováním, kdy nejprve zjednodušíme všechny paralelně řazené rezistory a nahradíme je jedním náhradním odporem.
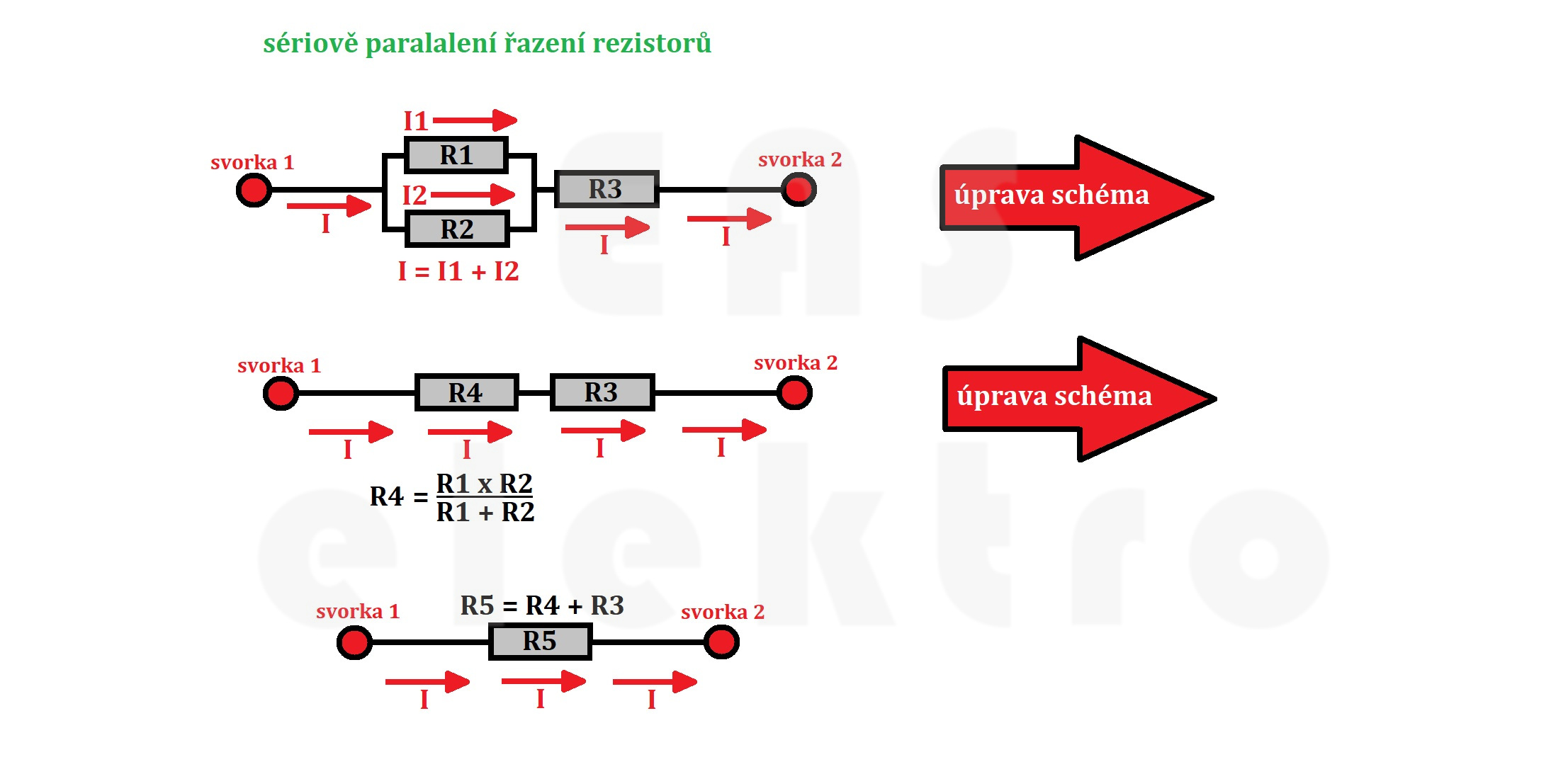
Tím vytvoříme sériově řazené schéma, které už snadno sečteme.
V následujícím příkladu si zkusíme zjednodušit jedno větší sérioparalelní schéma, kde R1 = 30Ω, R2 = 15Ω, R3 = 10Ω a napětí U je 230V.
Naším úkolem bude zjistit jaký proud prochází každým rezistorem a jednotlivé úbytky napětí mezi svorkami (uzly).
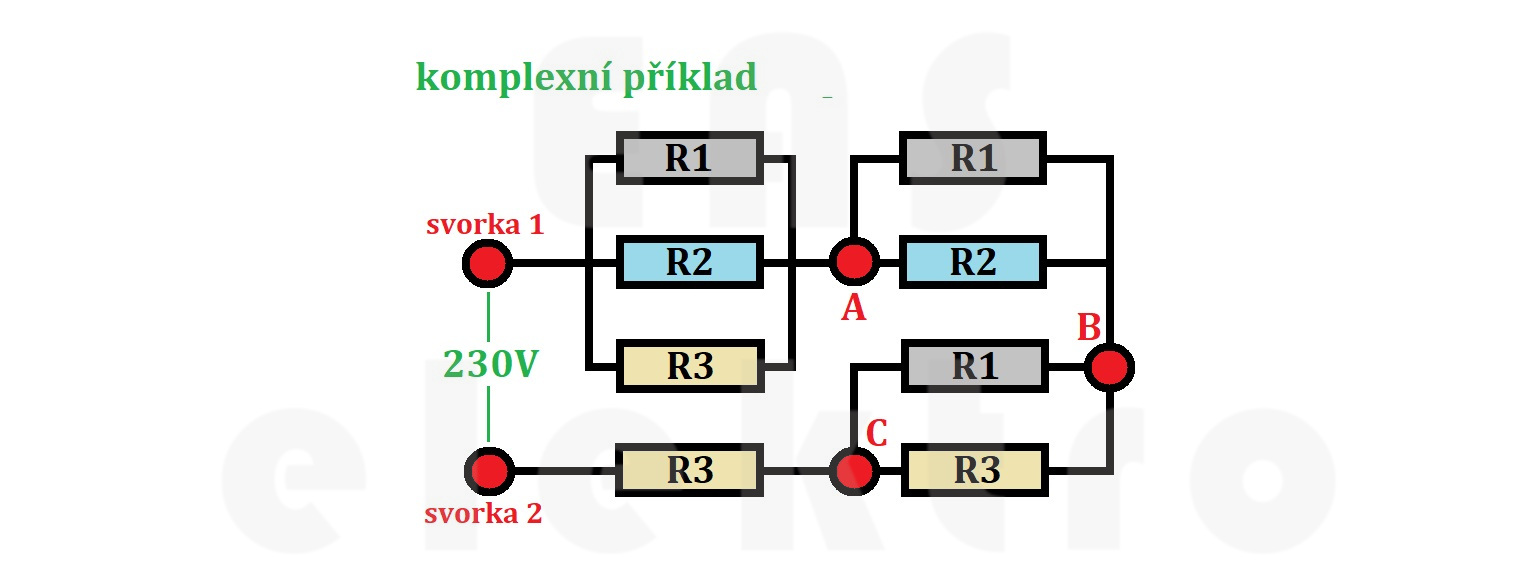
Začneme tím, že zjednodušíme všechny paralelně řazené rezistory pomocí náhradních odporů R4, R5 a R6.
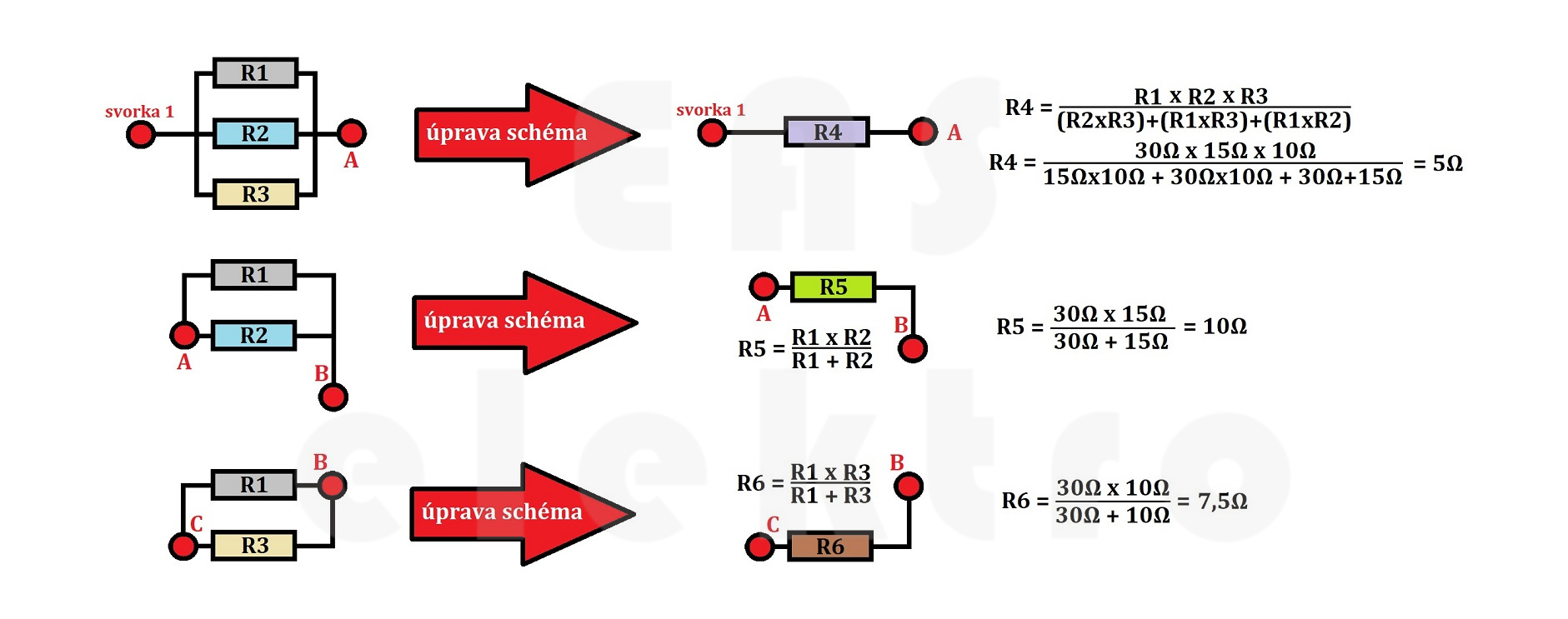
Podle vzorců z předchozích částí článku můžeme zjistit, že R4 = 5Ω, R5 = 10Ω a R6 = 7,5Ω a tyto odpory vytvoří sériově řazený obvod. Ty následně sečteme a zjistíme celkový odpor obvodu ve výši 32,5Ω.
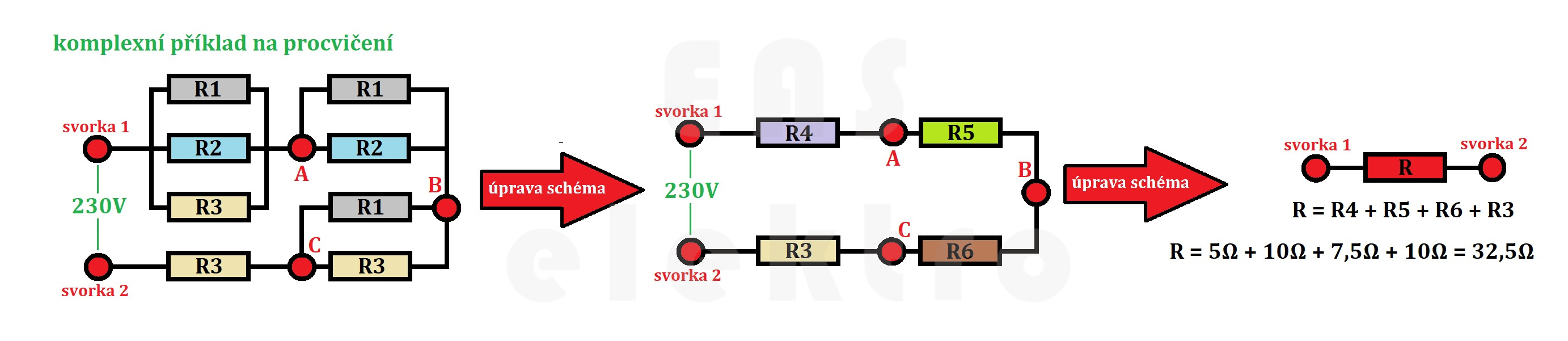
Díky znalosti celkového odporu 32,5Ω a napětí 230V zjistíme na základě Ohmova zákona celkový procházející proud obvodem ve výši 7,08A. Když už známe celkový proud a dílčí odpory mezi uzly, můžeme jejich součinem snadno stanovit jednotlivé úbytky napětí.
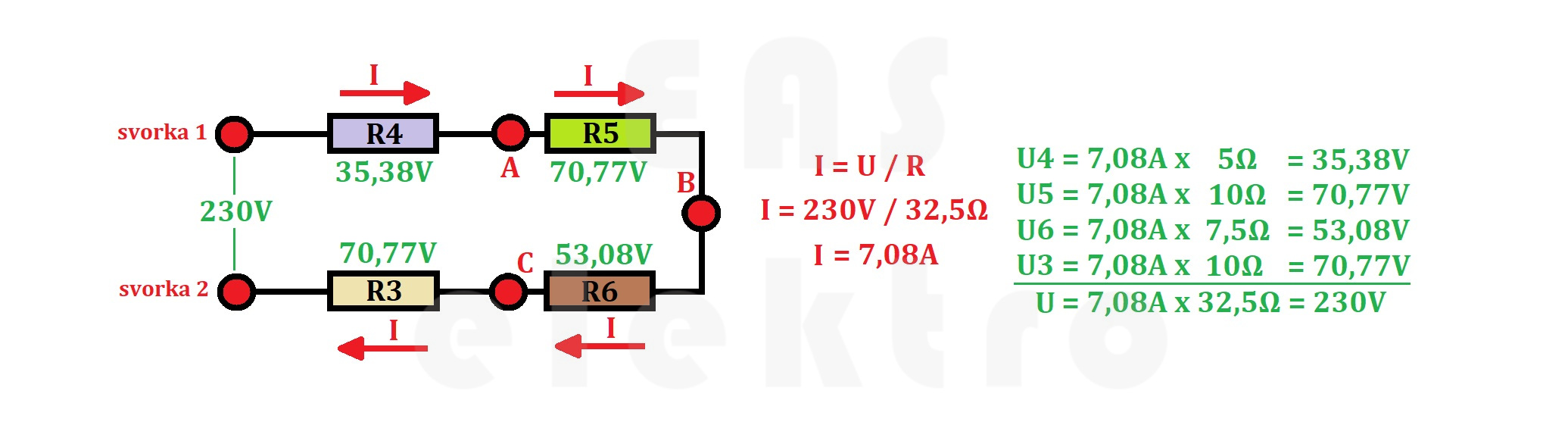
Při znalostech dílčích úbytků napětí zjistíme elektrický proud procházející jednotlivými odpory. Nezapomínáme, že součet proudů procházejících jednotlivými odpory se musí rovnat celkovému proudu I = 7,08A.
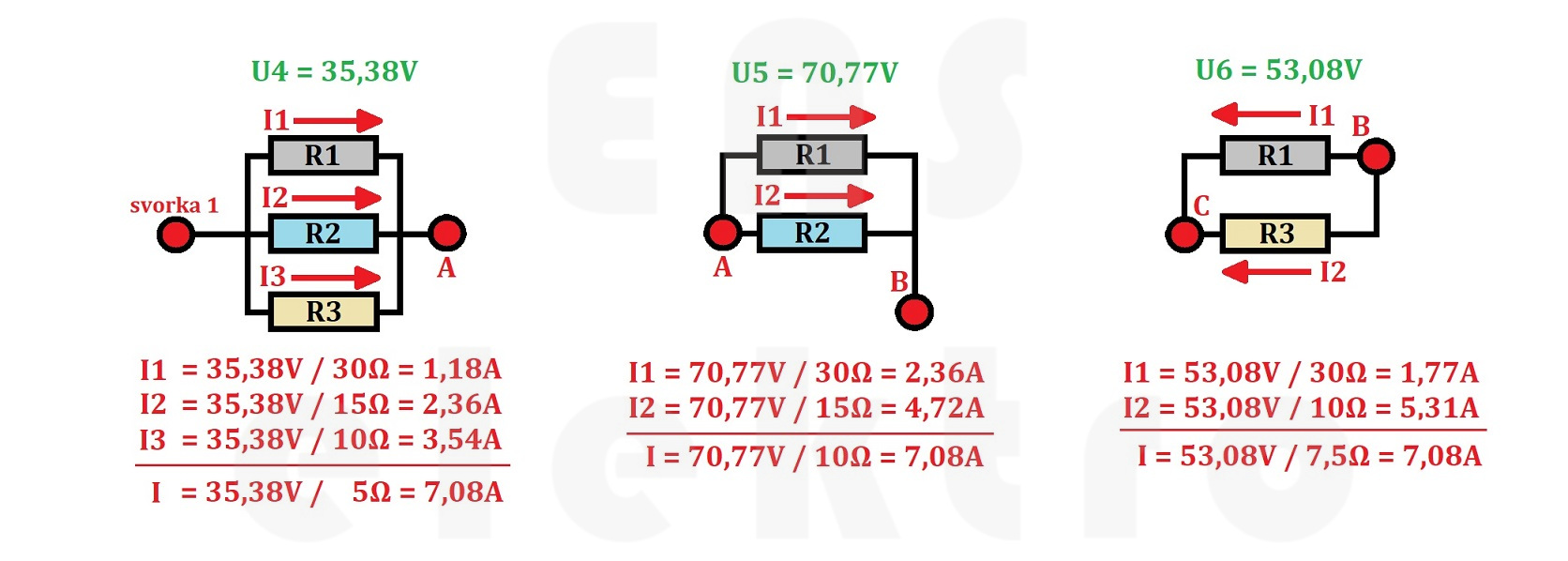
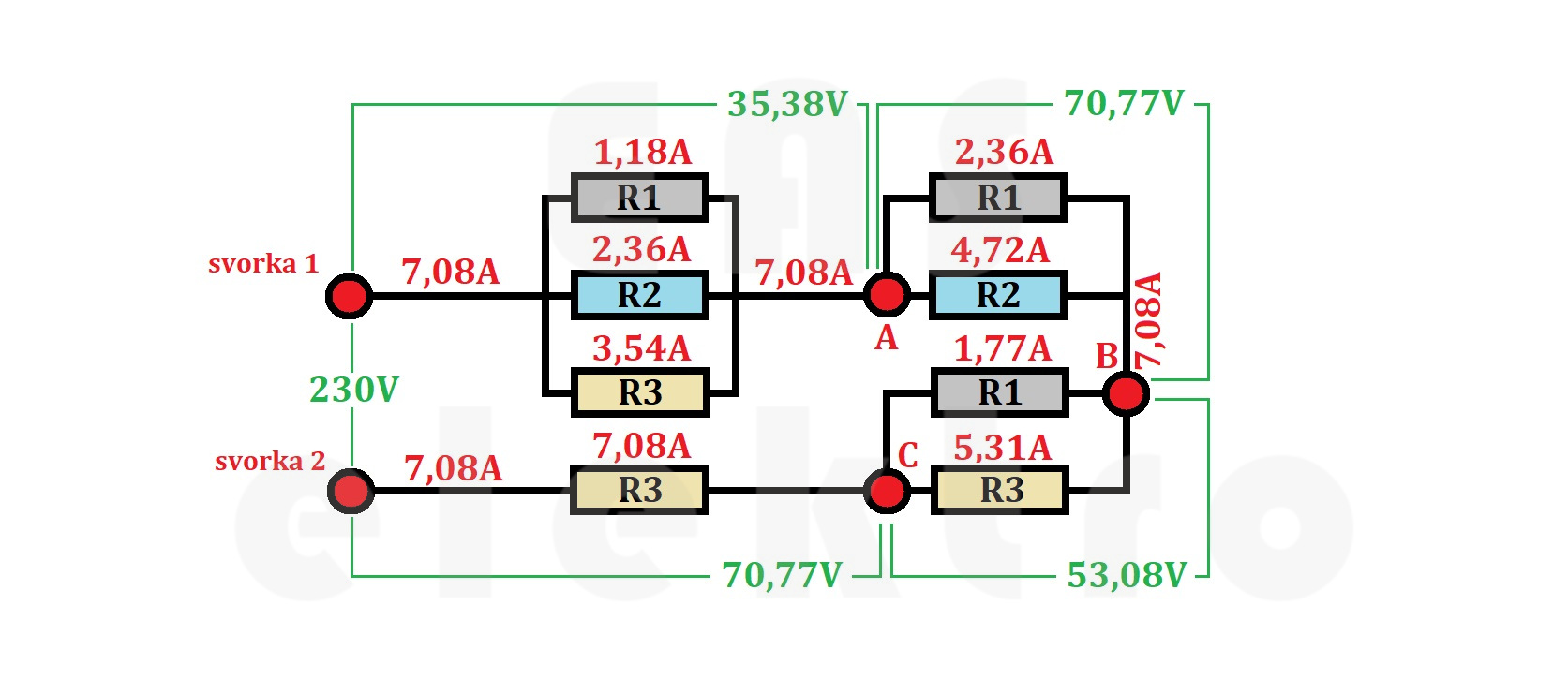
Nyní již známe všechny potřebné informace, abychom podrobně mohli popsat zadaný obvod a doplnit jednotlivé proudy k jednotlivým rezistorům a úbytky napětí mezi uzly (svorkami).
Všimněte si, že ačkoliv odpor R1 = 30Ω, tak jednou jím prochází 1,18A, jindy 2,36A a nakonec 1,77A. Totéž platí i pro další odpory.
Kromě sériových nebo paralelních řazení rezistorů, popř. jejich kombinací, existují i složitější schémata, která výše uvedenými postupy řešit nelze. Jedním z takových případů je následující schéma, které díky propoji mezi svorkou 2 a 3 není sériovým, paralelním a ani sérioparalelním řazením.
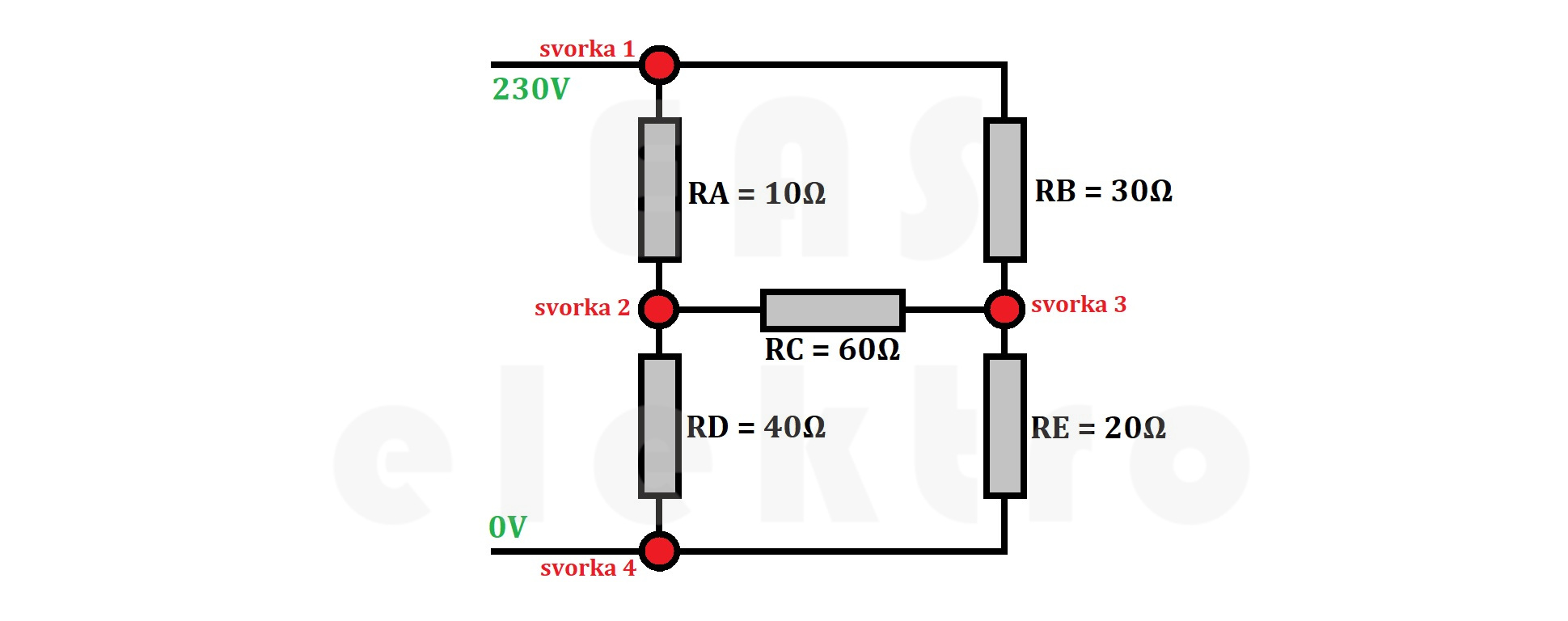
Jedná se vlastně o schéma s dvěma trojúhelníky, a i takové schéma lze řešit. Způsob, který toto řešení umožňuje se nazývá transfigurace trojúhelníku na hvězdu a je včetně příkladu vysvětlen v tomto článku.
Pokud jste v článku nalezli chybu, dejte nám, prosíme, o ní vědět na eas@eas-elektro.cz
Děkujeme, Eva a Aleš Smetákovi - návrat zpět na přehled článků