26.11.2023 - Ing. Aleš Smeták
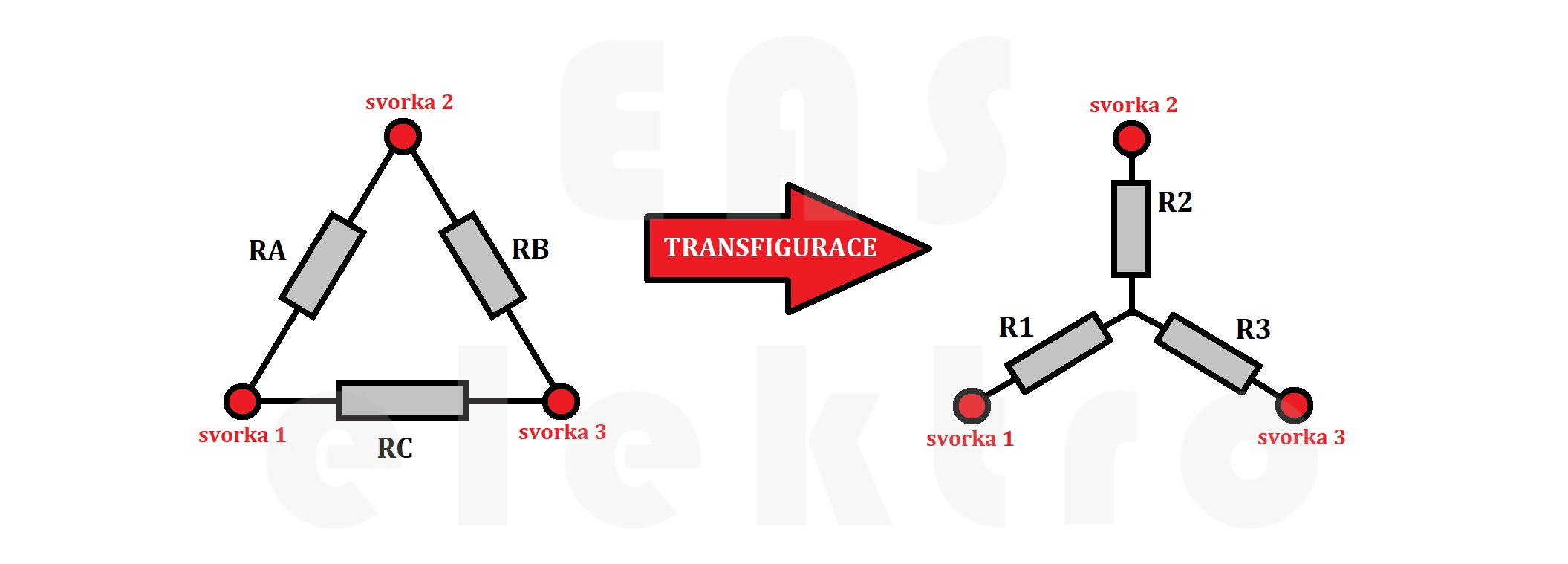
Transfigurace / transformace z trojúhelníku (Δ) do hvězdy (y) nebo naopak je speciální úprava elektrického obvodu, při které za účelem jeho zjednodušení pro výpočet změníme jeho schéma zapojení.
Tím se nám schéma obvodu zjednoduší a umožní nám výpočet procházejících proudů i úbytků napětí na jednotlivých větvích obvodů, u kterých bychom se standardními poučkami pro sériové nebo paralelní zapojení nepochodili.
Transfiguraci můžeme využít pro výpočet parametrů složitých obvodů s odpory, které nejsou řazeny ani sériově a ani paralelně. Takovým typickým příkladem je zapojení odporů do trojúhelníku (označovaného jako zapojení D nebo Δ).
Pokud bychom chtěli zjistit odpor R1, tak to se nám to bez znalosti transfigurace trojúhelník / hvězda nepodaří.
Z obrázku níže je zřejmé, že odpor mezi svorkami 1 a 2 je vždy stejný, a to bez ohledu na to, zda je zapojení zařízení do trojúhelníku nebo do hvězdy. To samé platí pro odpor mezi svorkami 2 a 3 a samozřejmě i pro odpor mezi svorkami 3 a 1. Této skutečnosti při výpočtu dále využijeme.
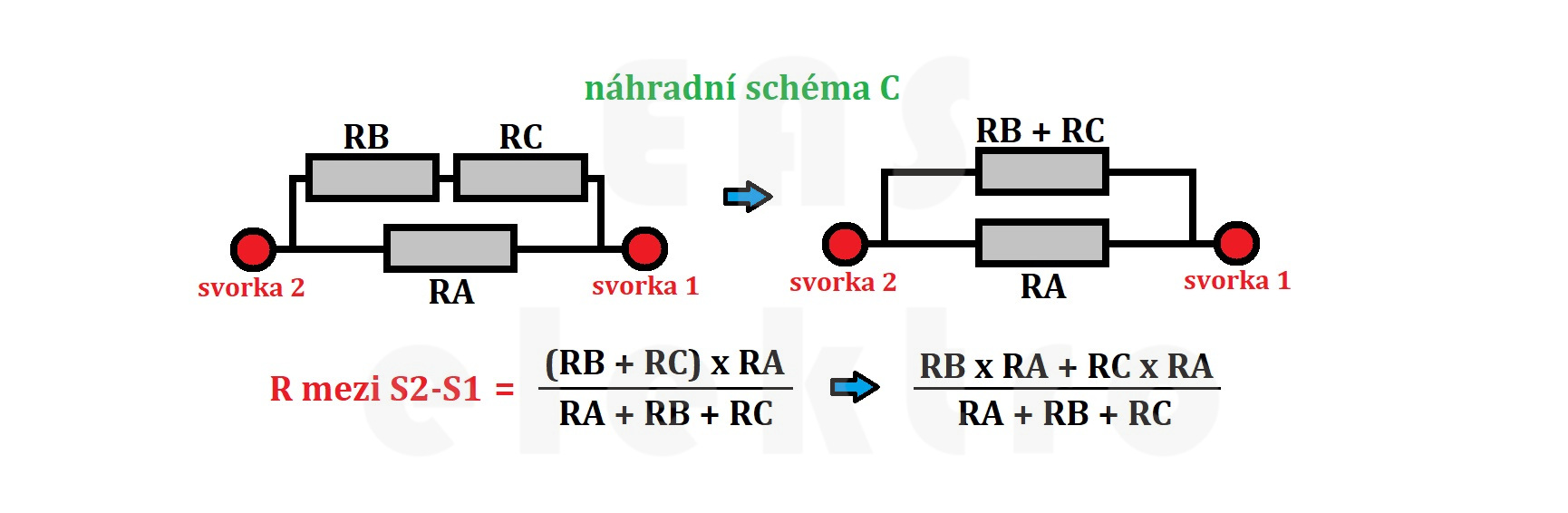
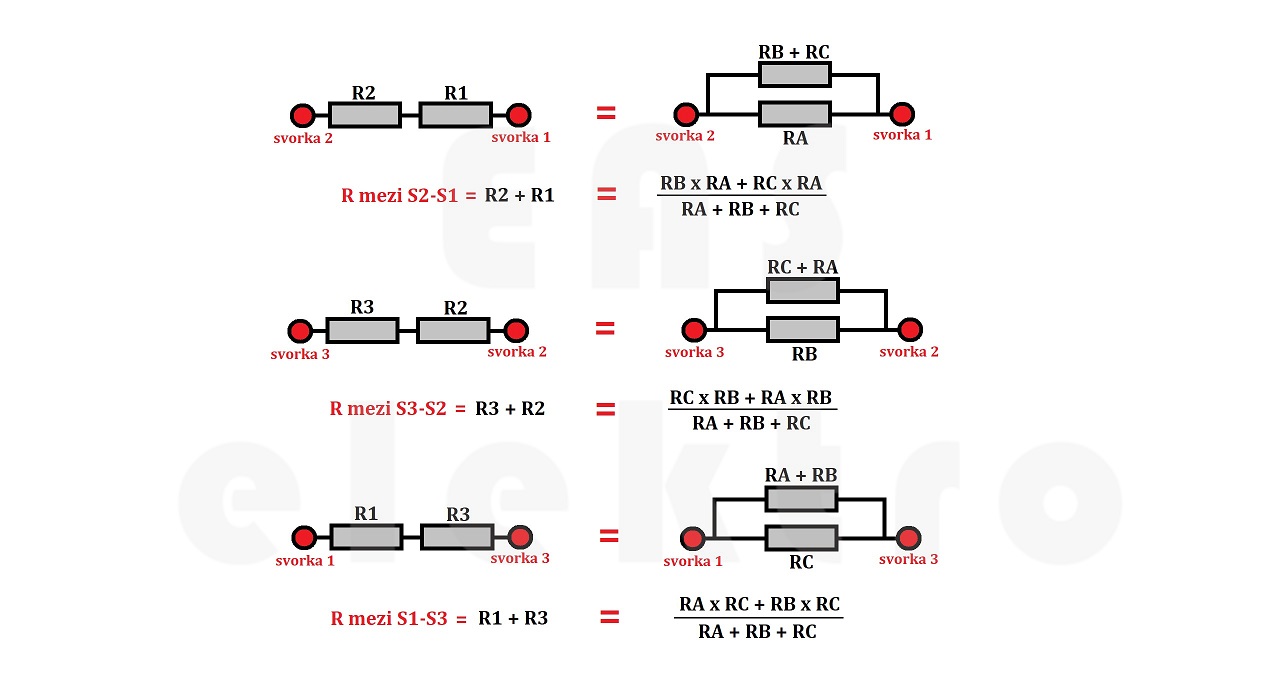
Odpory mezi jednotlivými svorkami můžeme zjistit pomocí náhradních schémat jednotlivých stran trojúhelníku Δ, která jsou již snadno řešitelná sériově-paralelní zapojení.
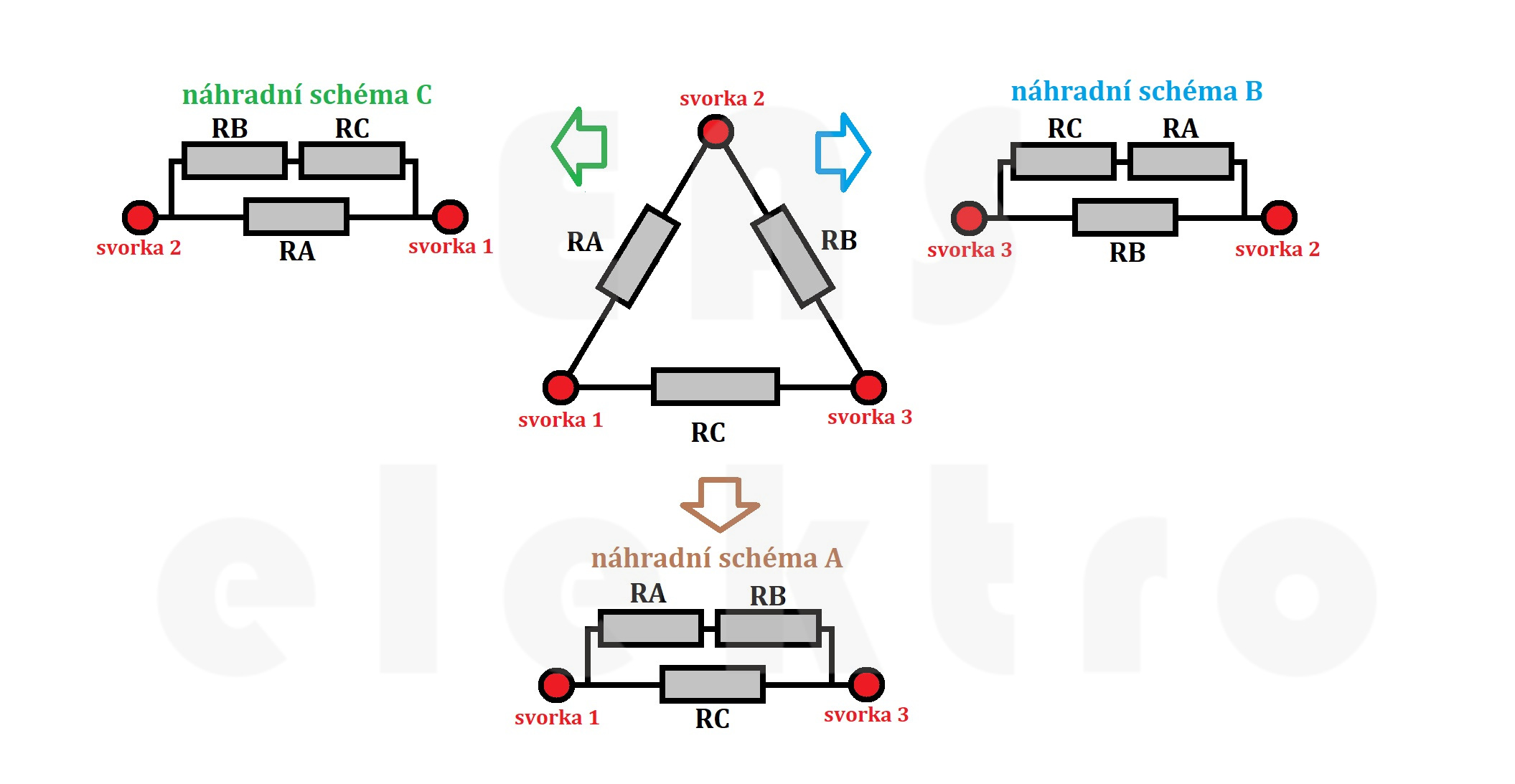
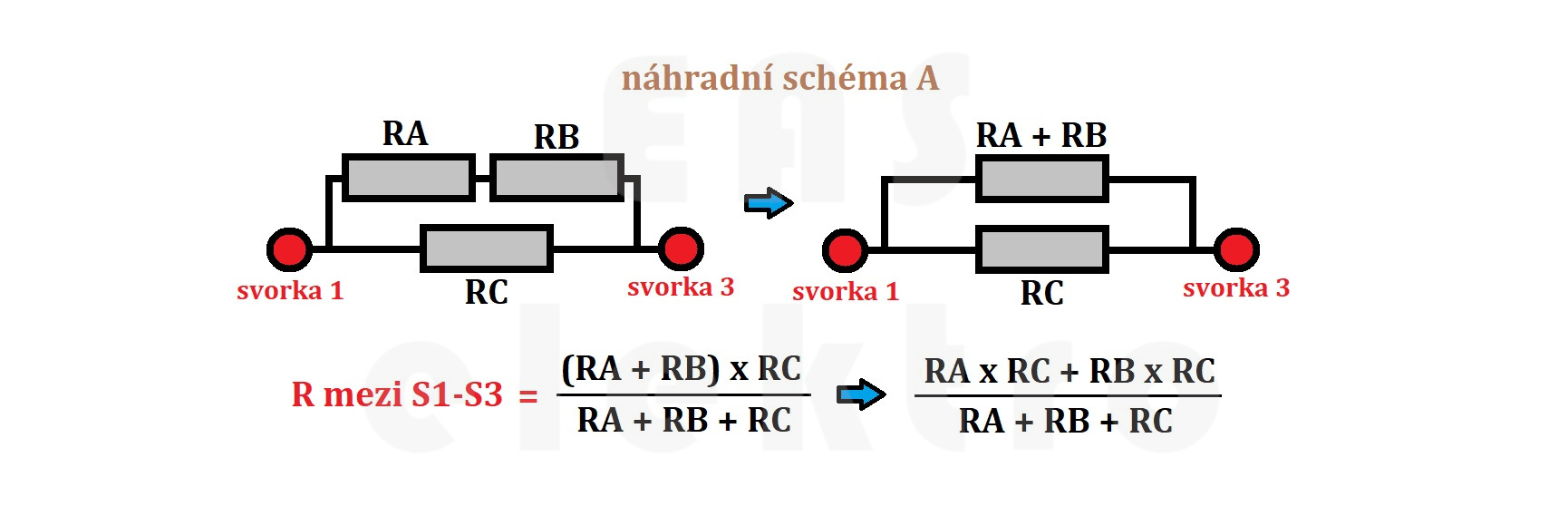
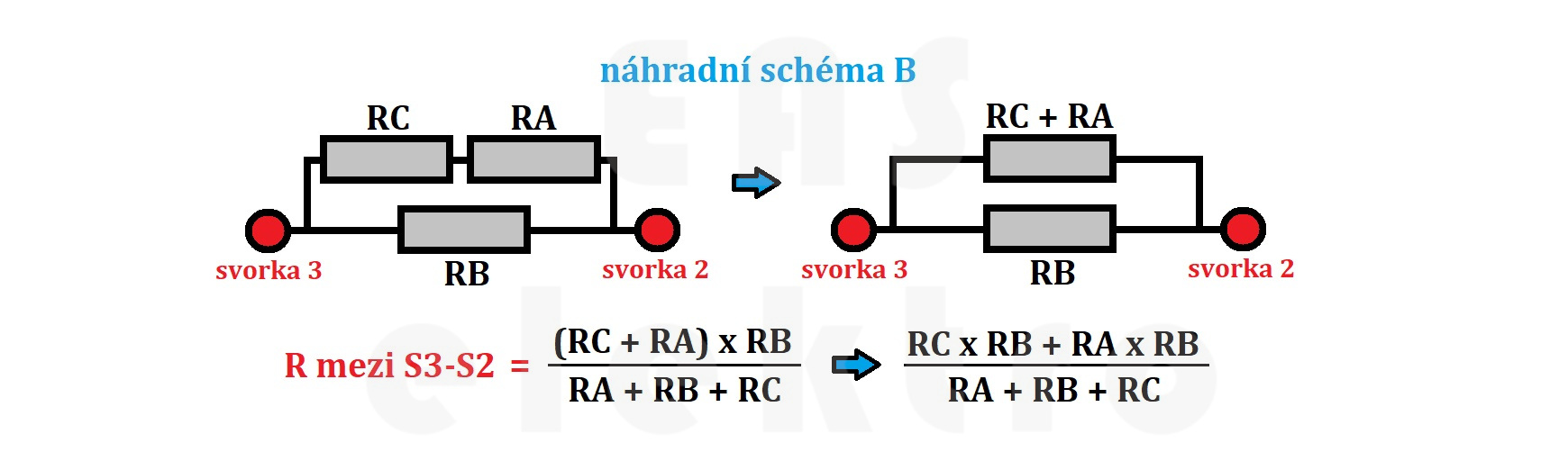
Jednotlivá náhradní schémata můžeme ještě zjednodušit podle následujících obrázků a matematicky vyjádřit odpor mezi jednotlivými svorkami. Tématu jak zjednodušovat obvody se věnuje tento článek.
To samé můžeme provést i pro schéma "hvězda", které také bývá označované jako "Y".

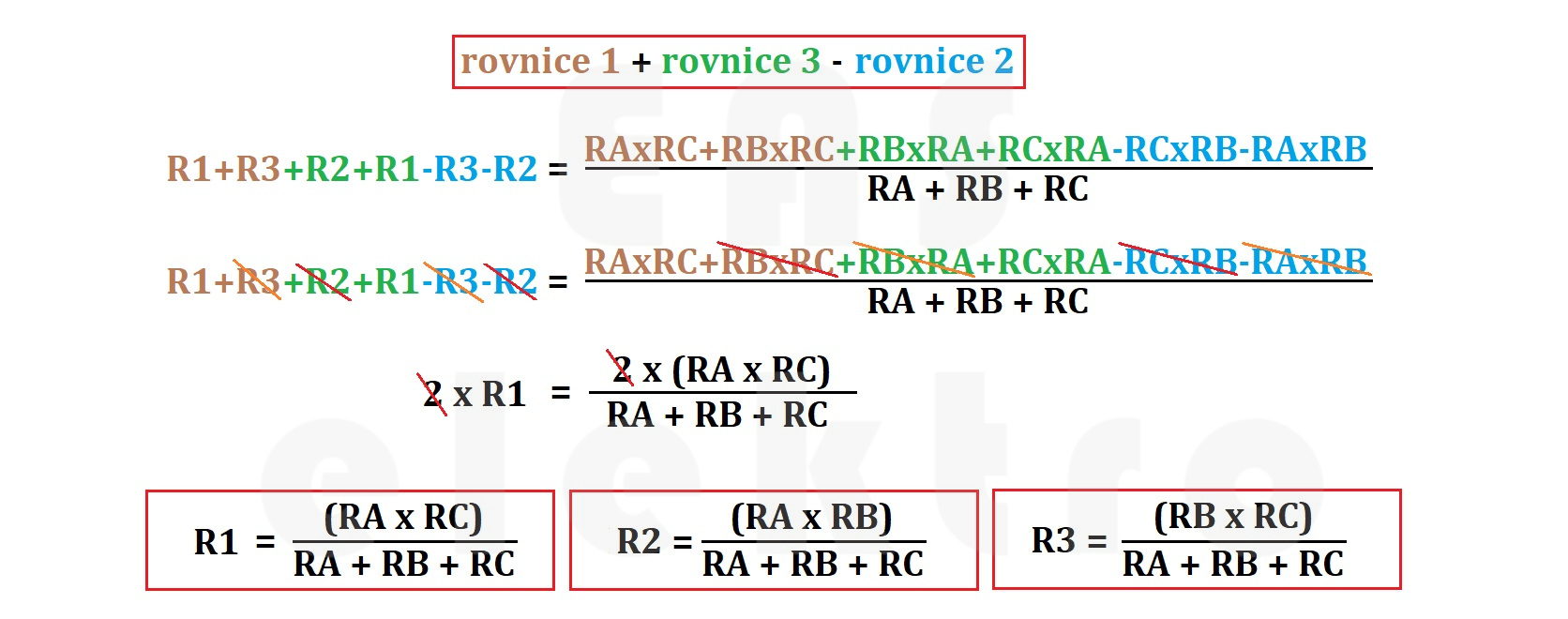
Nyní známe všechna matematická vyjádření odporů mezi jednotlivými svorkami, a to jak pro zapojení v trojúhelníku, tak ve hvězdě. Celkem tedy máme šest různých výrazů, které tvoří tři rovnice a ty zase tvoří jednu soustavu rovnic.

Nakonec stačí vyřešit soustavu rovnic a získáme výraz nejen pro výpočet odporu R1 ale pro R2 a R3.
Transfigurace z hvězdy (Y) na trojúhelník (Δ) nedává výpočtově takový smyl jako transfigurace z trojúhelníku (Δ) na hvězdu (Y), protože místo zjednodušení obvodu ho děláme složitějším, ale i tak si ukážeme jak na to.

I v případě této transfigurace platí soustava rovnic z předchozího odvození, protože, jak jsme si již řekli, odpor mezi svorkami 1 a 2, 2 a 3, 3 a 1 je pořád stejný, a to bez ohledu na schéma zapojení.
Pokud bychom tedy chtěli odvodit vzorec pro stanovení odporu RA, museli bychom si ho ze soustavy doslova vypreparovat, a to z výše uvedené soustavy není zrovna jednoduché. Ale fungovalo by to...
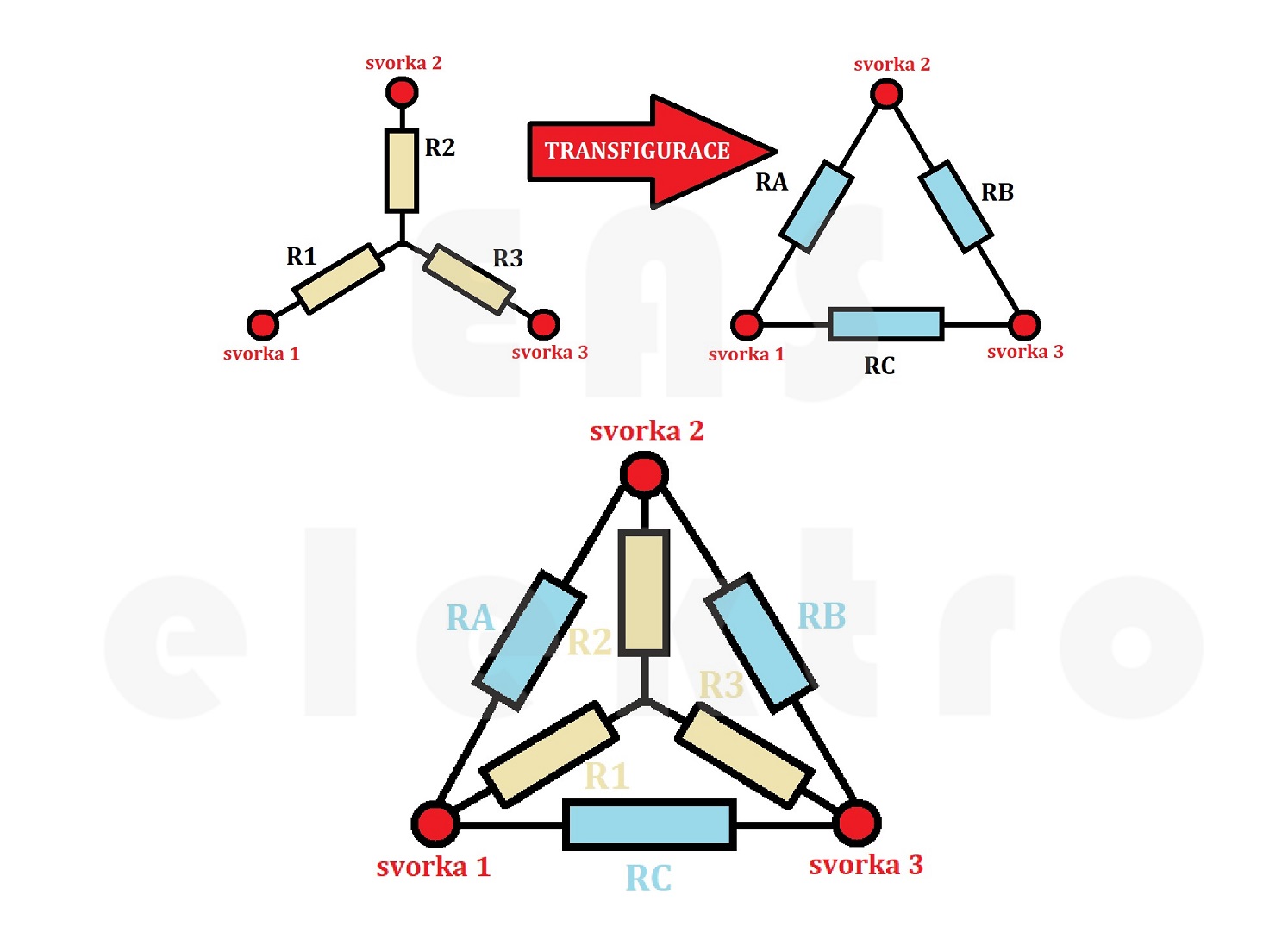
Mnohem jednodušší bude jít na to od lesa a uvědomit si, že odpor RA lze získat jako součet součinů všech párů odporů na vývodech hvězdy (Y) a podělit ho protilehlým odporem. Z výše uvedeného obrázku je zřejmé, že v případě hledaného odporu RA v trojúhelníku (Δ) je protilehlý odpor ve hvězdě (Y) R3.
Ono je konec konců jedno, jak si jednotlivé odpory a svorky v kterém schématu pojmenujete a důležité jen je, abyste toto pojmenování drželi celou dobu stejné.
Po úpravě zmíněné rovnice získáme následující výrazy pro odpory v trojúhelníku (Δ) RA, RB a RC.
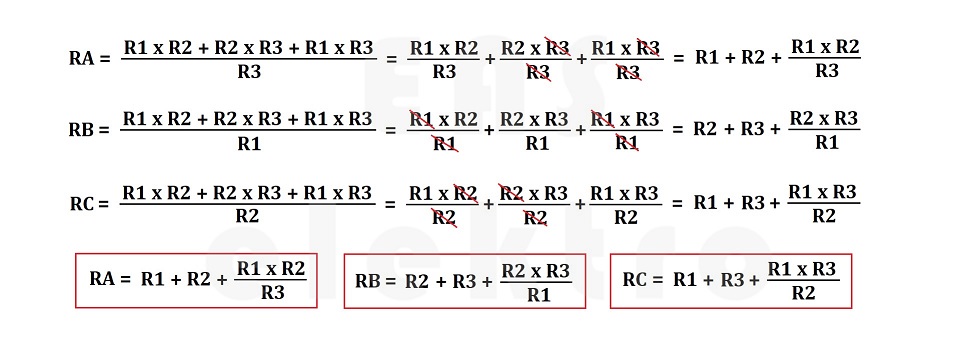
Na základě předchozích dvou kapitol víme, že pro výpočet jednotlivých odporů R1, R2 a R3 ve schématu hvězda (Y) a RA, RB a RC ve schématu trojúhelník (Δ), můžeme použít následujících vzorců...
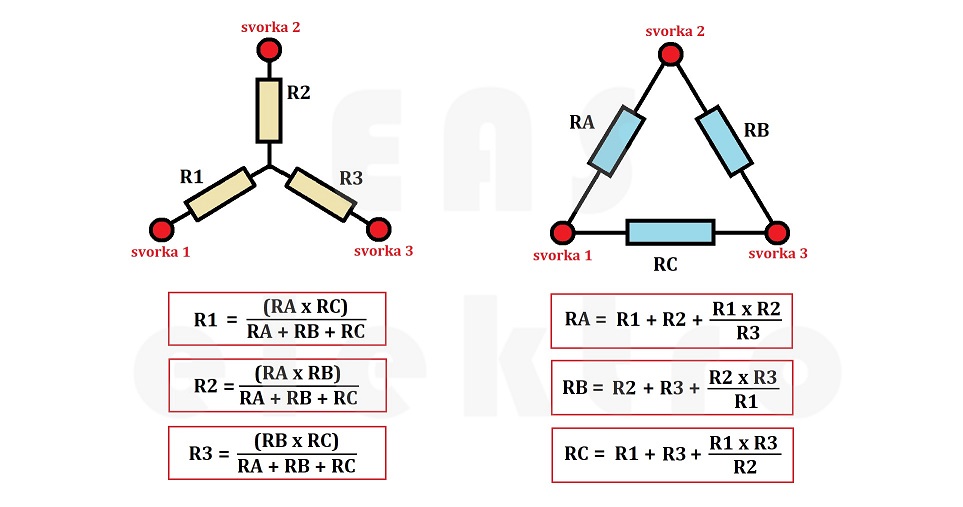
Také víme, že výpočet odporů mezi jednotlivými svorkami můžeme stanovit podle následujících náhradních schémat, a že tyto jednotlivé odpory musí nabývat stejných hodnot bez ohledu na to, jestli je počítáme v trojúhelníku (Δ) nebo ve hvězdě (Y).
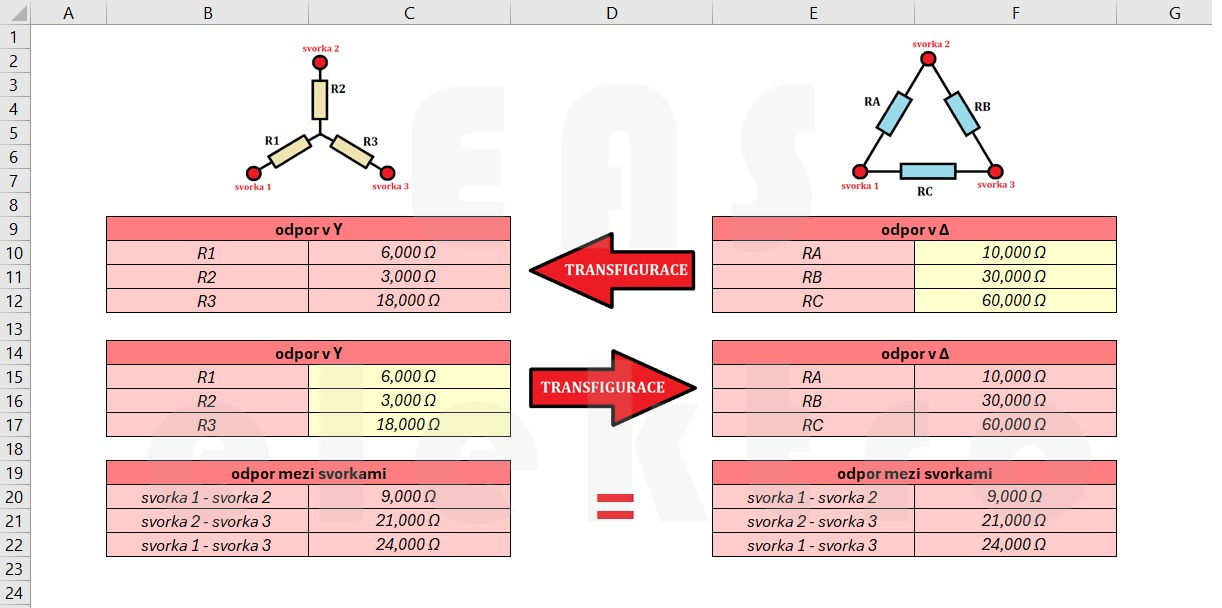
Nyní si zkusme pár příkladů. Pro zjednodušení jsem výpočty počítal v Excelu, ale použité vzorce přesně odpovídají obrázkům výše.
V prvním příkladu si odpory v trojúhelníku stanovíme na RA = 10 Ω, RB = 30 Ω a RC = 60 Ω. Po dosazení do vzorců nám vychází odpory ve hvězdě R1 = 6 Ω, R2 = 3 Ω a R3 = 18 Ω.
Pokud bychom tyto odpory naopak dosadili do vzorců pro transfiguraci z Y na Δ, vyjdou nám zase původní hodnoty RA = 10 Ω, RB = 30 Ω a RC = 60 Ω. Můžeme si také ověřit, že odpory mezi jednotlivými svorkami jsou stejné bez ohledu na to, v jakém schématu je počítáme.
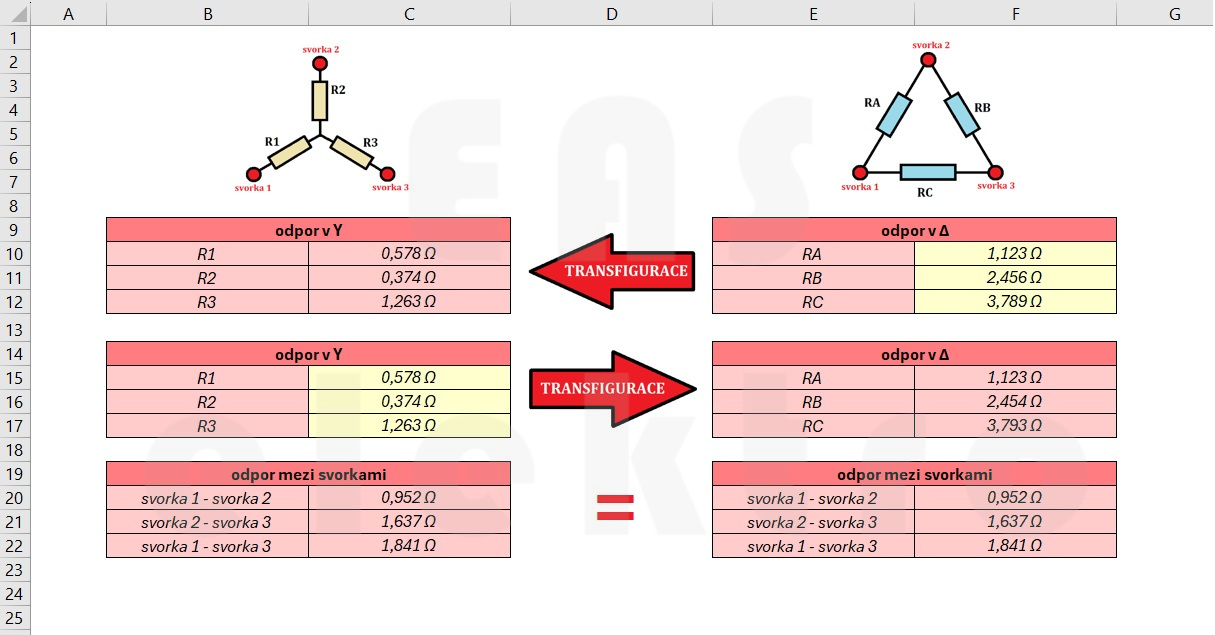
V druhém příkladě si odpory v trojúhelníku zvolíme všechny stejné RA = RB = RC = 3 Ω. Po dosazení do vzorců nás nemůže překvapit, že i odpory ve hvězdě vychází stejné, R1 = R2 = R3 = 1 Ω.
Pokud bychom tyto odpory naopak dosadili do vzorců pro transfiguraci z Y na Δ, vyjdou nám zase původní hodnoty RA = RB = RC = 3 Ω. Můžeme si také ověřit, že odpory mezi jednotlivými svorkami jsou stejné bez ohledu na to, v jakém schématu je počítáme.

V posledním příkladu záměrně volím nehezká čísla, aby bylo lépe vidět, že vzorce opravdu počítají správně a že drobné rozdíly jsou způsobeny jen vnitřním zaokrouhlením Excelu.
Zkusme si nyní jeden praktický příklad, který jsme představili již v předchozí kapitole. Máme níže uvedené schéma, ve kterém zařazeno pět odporů a toto téma nelze řešit pomocí zjednodušování sériových a paralelních obvodů, a k jehož vyřešení využijeme transfiguraci z trojúhelníku (Δ) na hvězdu (Y).
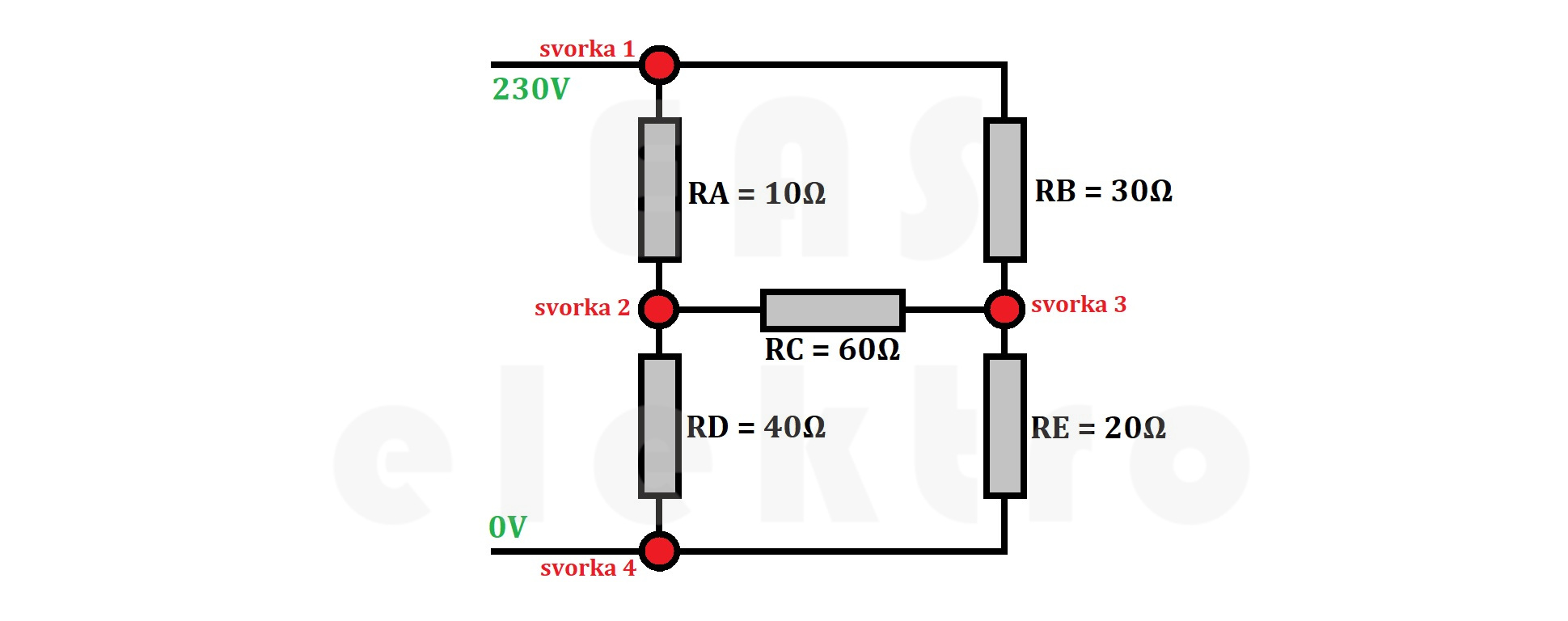
Na první pohled tam vidíme dvě trojúhelníková schémata - RA, RB a RC nebo RC, RD a RE. My si vybereme pro transfiguraci trojúhelník RA, RB a RC, ale fungovalo by to úplně stejně i pro ten druhý trojúhelník.
Schéma pomocí transfigurace převedeme z trojúhelníku na hvězdu a odpory RD a RE ponecháme zatím bez povšimnutí. Pro další výpočty si přidáme do středu hvězdy další svorku - svorka č.5.
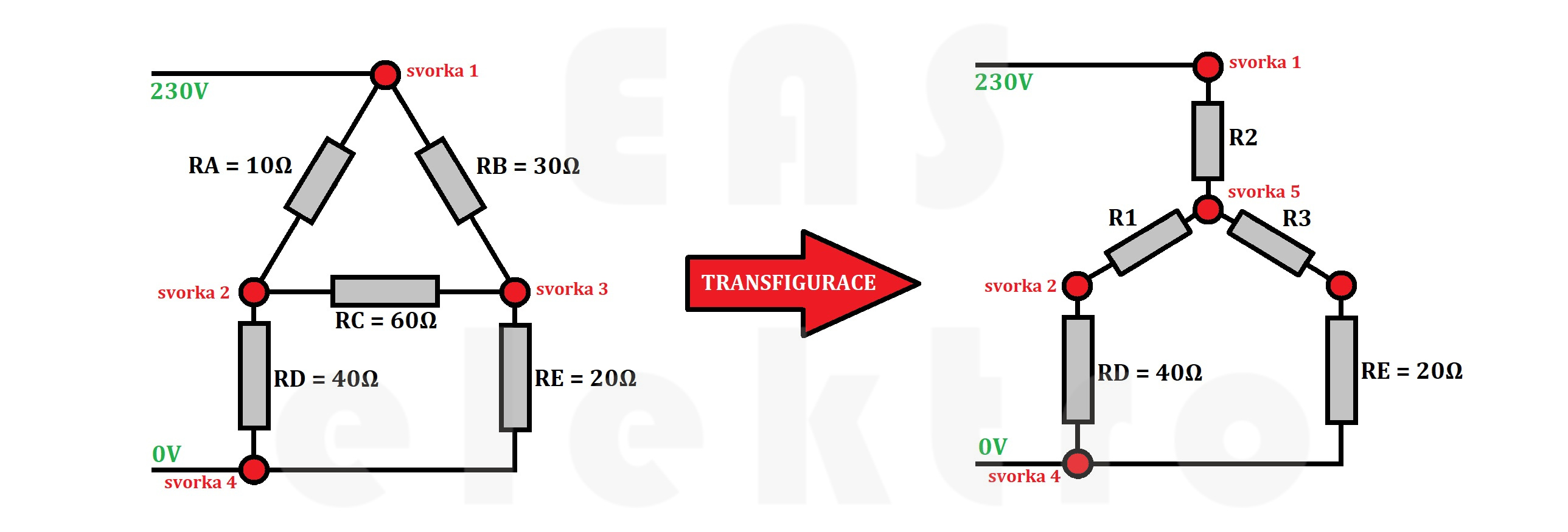
Po převedení trojúhelníku na hvězdu nám vznikly tři nové odpory R1, R2 a R3, které musíme vypočítat podle vzorců odvozených v první kapitole.
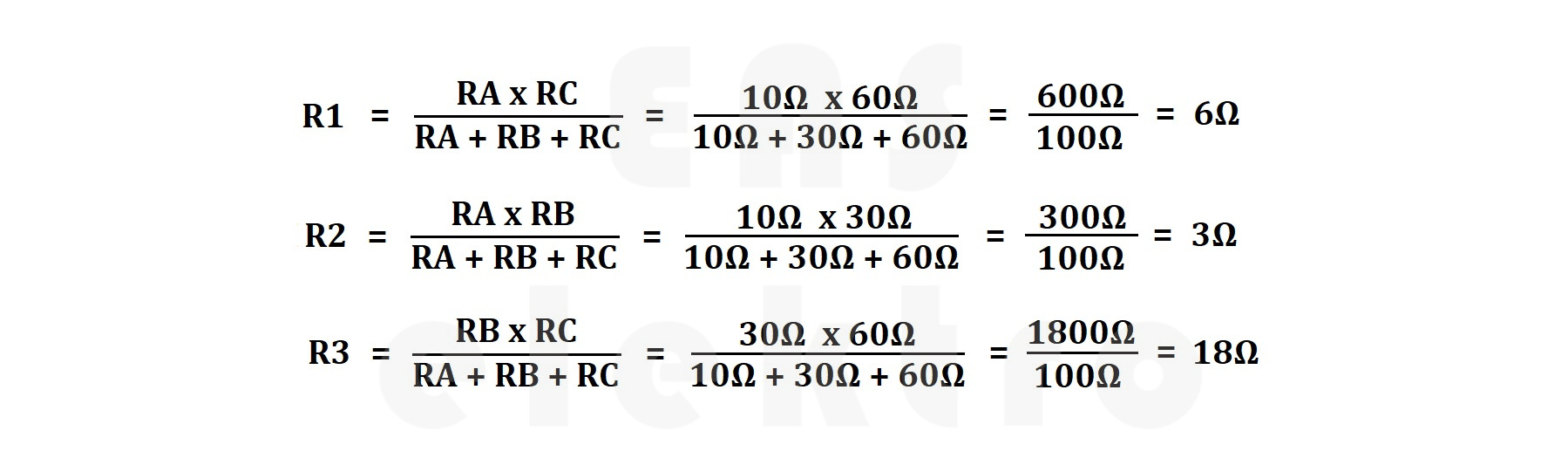
Při znalosti odporů R1, R2 a R3 můžeme již zjednodušit celé schéma sériově-paralelní obvod s odpory R2, RF a RG a ten dále na sériový obvod s R2 = 3Ω a RH 20,81Ω.

Nyní již, kromě celkového napětí 230V, známe celkový odpor obvodu ve výši 23,81Ω a díky Ohmovu zákonu můžeme stanovit celkový proud 9,66A tekoucí obvodem.

Dále samozřejmě můžeme stanovit jednotlivé úbytky napětí mezi svorkami 1 a 5 a mezi svorkami 5 a 4. Můžeme také snadno stanovit proudy procházející jednotlivými větvemi.
Pokud jste v článku nalezli chybu, dejte nám, prosíme, o ní vědět na eas@eas-elektro.cz
Děkujeme, Eva a Aleš Smetákovi - návrat zpět na přehled článků